Kraft
Das Wort Kraft ist altgermanischen Ursprungs. Im Deutschen bezeichnet Kraft eine körperliche oder geistige Voraussetzung zu bestimmten Handlungen (Muskelkraft; Geisteskraft; Manneskraft), die Ausführung der Tätigkeit selbst (eine Kraft ausüben; unter der Kraft zusammenbrechen) oder einzelne Akteure (Arbeitskraft, Schreibkraft, Streitkraft, die fortschrittlichen Kräfte). In der Rechtssprache bedeutet Kraft auch Gültigkeit (in Kraft setzen, rechtskräftig).
Als physikalischer Fachbegriff wurde Kraft von Archimedes eingeführt und von Galileo Galilei aufgegriffen. Bis weit ins 19te Jahrhundert benutzten Physiker das Wort Kraft jedoch auch im Sinne von Energie (bewegende Kraft, lebendige Kraft). Diese Bedeutung lebt heute noch in vielen Begriffen weiter (Kraftwerk, Kraftstoff, Kraftfutter).
Die Systemphysik gibt eine zeitgemässe Definition des klassischen Kraftbegriffs: Eine Kraft ist eine Impulsstromstärke oder eine Impulsquellenstärke bezüglich eines ausgewählten Systems. Eine Kraft verändert den Impulsgehalt eines Körpers und damit auch seinen Bewegungszustand, die Geschwindigkeit seines Massenmittelpunkts. Aus dieser Definition sind alle anderslautenden, korrekten Definition der klassischen Mechanik ableitbar
Die Physik des 20. Jahrhunderts hat den Kraftbegriff weiter umgestaltet. Heute versteht man unter den Grundkräften die vier Fermionenfelder:
Der Kraftbegriff der modernen Physik lässt sich nur im Rahmen der Quantenfeldtheorie sauber erklären: Fermionen- und Bosonenfelder tauschen untereinander Impuls, Drehimpuls, elektrische Ladung und Entropie aus. Weder die starke noch die schwache Wechselwirkung lassen sich auf Systeme anwenden, welche den Gesetzen der klassischen Mechanik gehorchen. Diese beiden Wechselwirkung sind nicht mit der Newton-Eulerschen Theroie des starren Körpers verträglich und sollten in diesem Zusammenhang auch nicht erwähnt werden.
Kraft und Impuls
Eine Kraft ist eine Impulsstromstärke oder eine Impulsquellenstärke bezüglich eines Systems. Eine Kraft bezieht sich also immer auf einen Körper, Kräfte sind keine eigenständige Objekte der Natur. Aus diesem Grund muss man einen Körper freischneiden, um die Kräfte korrekt einzuzeichnen.
Impulsströme treten über die Oberfläche, Impulsquellen koppeln an das Gravitationsfeld oder das elektromagnetische Feld. Der Kraftpfeil beschreibt nur die Stärke des Impulsstromes oder der Impulsquelle. Der Kraftpfeil sagt nichts über die Richtung, in die der Impuls transportiert wird.
Die Kraft wird in Newton (N; 1 N = 1 kgm/s2) gemessen. Als Formelzeichen verwenden wir F oder (Fx, Fy, Fz).
eindimensional
Der Kraftpfeil zeigt entweder in oder gegen die Bezugsrichtung. Zeigt der Kraftpfeil in Bezugsrichtung, fliesst Impuls in den fraglichen Körper hinein, zeigt er gegen die Bezugsrichtung, fliesst der Impuls aus dem Körper heraus. Diese Aussage kann in zwei Merksätzen formuliert werden
- ein zufliessender Impulsstrom ergibt eine positive Kraft, ein abfliessender Impulsstrom ergibt eine negative Kraft
- ein in die positive Richtung weisender Kraftpfeil symbolisiert die Stärke eines zufliessenden Impulsstromes, ein in negative Richtung weisender Kraftpfeil steht für die Stärke eines abfliessenden Impulsstromes
Beispiel
- Ein Traktor zieht einen Wagen in Richtung der positiven Achse des Koordinatensystems weg. Die Stärke des vom Traktor über die Deichsel in den Wagen fliessenden Impulsstromes wird bezüglich des Wagens als nach vorne gerichteter Kraftpfeil und bezüglich des Traktors als nach hinten gerichteter Kraftpfeil dargestellt.
- Ein Auto fährt in Richtung der positiven x-Achse an und bremst sofort wieder ab. Sieht man vom Luftwiderstand ab, zeigt der (Haftreibungs-)Kraftpfeil in der ersten Phase nach vorne und in der zweiten nach hinten. Die Pfeile zeigen horizontal, der x-Impuls fliesst an der Schnittstelle zwischen Rad und Strasse aber in vertikaler Richtung.
- Ein Boxer schlägt dem Gegener mit seiner rechten Faust voll auf die Brust. Die Stärke des zeitabhängigen Impulsstromes wird mit einem zeitabhängigen Kraftpfeil auf die Brust (Zufluss) und mit einem zu jedem Zeitpunkt entgegengesetzt gleichen Kraftpfeil (Abfluss) auf die Faust dargestellt.
dreidimensional
Ein raumfestes Koordinatensystem zerlegt den Impuls in drei Komponenten oder "Sorten". Folglich können bezüglich einer beliebigen Querschnittfläche drei verschiedene Impulsströme gemessen werden. Die Stärken dieser drei Impulsströme heissen Kraftvektor, falls die Impulsströme durch die Oberfläche eines Körpers fliessen. Der Kraftvektor kann aber auch für die Quellenstärke der drei Impulskomponenten stehen. Zwischen den Stromstärken der drei Impulskomponenten und den entsprechenden drei Komponenten der Kraft besteht folgender Zusammenhang:
- ein zufliessender x-, y- oder z-Impulsstrom ergibt eine positive x-, y- oder z-Kraft, ein abfliessender x-, y- oder z-Impulsstrom ergibt eine negative x-, y- oder z-Kraft
- eine in die postive x-, y- oder z-Richtung weisende Kraftkomponente symbolisiert die Stärke eines zufliessenden x-, y- oder z-Impulsstromes, ein in negative x-, y- oder z-Richtung weisende Kraftkomponente steht für die Stärke eines abfliessenden x-, y- oder z-Impulsstromes'
Im elementaren Physikunterricht arbeitet man meist nur mit Seilen und Pendelstützen. Da diese Bauteile nur in Richtung ihrer Längsachse (einachsig) belastet werden, zeigen die Kraftpfeile immer längs des Seils oder der Pendelstütze. Eine solche Visualisierung des Kraftbegriffs mittels Seilen erschwert den tieferen Einstieg in die Mechanik, auch wenn sie den Anfängern einen anschaulichen Kraftbegriff zu vermitteln vermag.
In der technischen Mechanik spricht man auch von inneren Kräften. Um diese Kräfte "sichtbar" zu machen, schneidet der Ingenieur das belastete Bauteil entzwei und weist der Stärke des durchfliessenden Impulsstromes einen Kraftpfeil zu. Um die Richtung des Kraftpfeiles eindeutig festzulegen, muss der Ingenieur der Schnittfläche ein Schnittufer zuweisen. Faktisch handelt es sich dann nicht mehr um innere Kräfte, weil das Bauteil mit dem Schnitt in zwei Stücke zerlegt worden ist. Die beiden möglichen Schnittufer gehören dann zu den Oberflächen der beiden Stücke des Bauteils.
Wechselwirkungsprinzip
Der Kraftpfeil markiert mit seinen drei Komponenten die Stärken der entsprechenden Impulsströme bezüglich eines der beiden beteiligten Körper. Mit dieser Zuweisung ist das Wechselwirkungsprinzip abschliessen erklärt
- die Stärke eines Impulsstromes ist bezüglich der beiden beteiligten Systeme immer entgegengesetzt gleich gross
Newton hatte das Wechselwirkungsprinzip als eigenständige Aussage in seine Theorie eingefügt. Mit Hilfe des Wechselwirkungsprinzips kann die Erhaltung des Impulses im Rahmen der Punktmechanik bewiesen werden. Doch das ist Geschichte. Das Wechselwirkungsprinzip macht aus heutiger Sicht eine einfache Bilanzaussage: was zum einen System herausfliesst geht unmittelbar ins zweite hinein.
Gewichtskraft
Die Gewichts-, Schwer- oder Gravitationskraft beschreibt die Stärke der Impulsquelle im Körper drin. Diese Quellenstärke ist proportional zur (schweren) Masse (Körpereigenschaft) und proportional zur Stärke des Gravitationsfeldes (Raumeigenschaft)
[math]\vec F_G = m \cdot \vec g[/math]
Der volumenmässig (quellenartig) über das Gravitationsfeld zufliessende Impuls kann vollständig im Körper gespeichert (freier Fall) oder unmittelbar über die Körperoberfläche abgeführt werden (Statik). Weil die schwere und die träge Masse ununterscheidbar sind, weiss man bei den Impulsströmen bezüglich eines Körpers (Oberflächenkräfte) nie, welcher Anteil aus dem Körper kommt und welcher übers Gravitationsfeld zugeflossen ist. Diese Problematik wird unter dem Stichwort Einsteinlift eingehend besprochen.
Im inhomogenen Gravitationsfeld ist die Gewichtskraft über eine Integration über das ganze Volumen zu berechnen
[math]\vec F_G = \int \rho \cdot \vec g \cdot dV[/math]
Oberflächenkraft
Oberflächenkräfte sind Impulsstromstärken bezüglich der Oberfläche eines willkürlich festgelegten Systems (freizuschneidender Körper). Wie jede Stromstärke kann die Kraft (Impulsstromstärke) über ein Flächenintegral aus der Impulsstromdichte berechnet werden. Weil der Impuls selber ein Vektor ist, muss die Impulsstromdichte ein Tensor zweiter Stufe sein:
- die Impulsstromdichte entspricht bis auf das Vorzeichen dem Spannungszustand (Spannungstensor). Eine Oberflächenkraft ist folglich gleich dem mit Minus eins multiplierten Wert des Flächenintegrals über den Spannungstensors
[math]F_i = \int j_{pij}dA_j = {-}\int \sigma_{ij}dA_j[/math]
Sobald man sich mit ausgedehnten Systemen wie Brücken, Autos oder Flugzeuge und nicht nur mit Massenpunkten beschäftigt, hängt die Kraft von der willkürlich definierten Schnitt- oder Referenzfläche ab. Betrag und Richtung einer Kraft sind keine objektiven Grössen, weil man die Referenzfläche beliebig wählen kann, weil sich ein System beliebig in Teile zerschneiden lässt.
Beispiele
Klotz an einer Feder
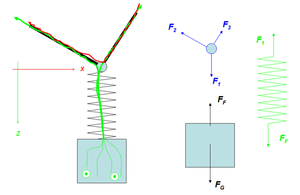
Ein Klotz hängt über Feder und Ring an zwei Seilen. Wir treffen nun die Annahme, dass nur der Klotz eine Masse besitze. Der Klotz befinde sich oberhalb der Gleichgewichtslage; die Feder ist also nur wenig gespannt. Im Moment kann sich der Klotz nach oben, nach unten oder gar nicht bewegen.
Im linken Bild sind die Impulsströme skizziert. Der z-Impuls fliesst aus dem Gravitationsfeld in den Klotz hinein (Impulsquelle). Weil ein Teil im Körper bleibt, nimmt dessen Impuls zu, wobei der Impulsinhalt des Klotzes im Moment kleiner, grösser oder gleich Null sein kann. Der Rest des gravitativ zufliessenden Impulses strömt direkt durch die Feder nach oben weg. Im Ring verzweigt sich der z-Impulsstrom und teilt sich auf beide Seile auf. Weil in den Seilen der z-Impuls seitwärts transportiert wird, induziert er einen x-Impulsstrom, der von rechts nach links fliesst. Die Impulserhaltung und das spezielle Systemverhalten der Seile legen die Stärken der einzelnen Impulsströme fest.
Rechts sind die Schnittbilder für Klotz, Feder und Ring gezeichnet. Die Summe über alle Kräfte eines Systems ergibt dessen Impulsänderungsrate. Es dürfen also nur gleichfarbige Kräfte miteinander verrechnet werden (gleichfarbige Kräfte gehören zum gleichen Vektorraum). Zwei verschiedenfarbige Kraftpfeile mit gleichem Namen bilden ein Wechselwirkungspaar (Actio gleich Reactio).
Kraftpfeile sind graphische Darstellungen der Impulsstromstärken. Im unteren Teil der Anordung entspricht jeder Kraftpfeil einer Stromstärke des z-Impulses. Beim Ring muss man die zwei Kräfte F2 und F3 zuerst in eine x- und eine z-Komponente zerlegen. Die beiden Komponenten entsprechen dann den Stromstärken der beiden Impuls"sorten".
Wenn man sich auf die Gleichgewichtssituation beschränkt, in die Feder und in die beiden Seile je einen Kraftpfeil einzeichnet und dann zeigt, dass die Vektorsumme der drei Pfeile Null ergibt, scheint der Kraftbegriff einfacher als das Impulsstrombild zu sein. Nur ist man dann unprofessionell vorgegangen (keine sauber definierten Schnittbilder), hat implizit eine undeklarierte Eigenschaft der Seile verwendet (der Kraftpfeil zeigt immer in Seilrichtung) und verkennt, dass eine Kraft keine reale Grösse sein kann. Ein Kraftpfeil ist nur ein momentanes Mass für die Stärke eines Transportes durch eine willkürlich festgelegte Referenzfläche.
Flugzeug
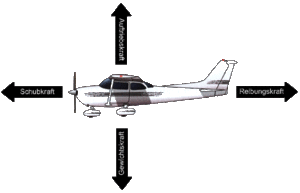
Ein Flugzeug kann Impuls mit dem Gravitationsfeld und mit der umgebenden Luft austauschen. Den Impulsaustausch mit dem Gravitationsfeld nennt man Schwer- oder Gewichtskraft. Den Impulsaustausch im Bereich des Antriebs (Propeller, Strahltriebwerk) markiert man mit einem Schubkraftpfeil und den restlichen Impulsaustausch mit der Luft zerlegt man bezüglich der Anströmung in einen Luftwiderstand und einen dynamischen Auftrieb. Den statischen Auftrieb, den geschwindigkeitsunabhängigen Impulsaustausch mit der Luft, berücksichtigt man in der Regel nicht.
Die Kraftdarstellung erlaubt eine einfache Abschätzung bezüglich Gleichgewicht und Anstellwinkel. Um die Details des Impulsaustausches zwischen Flugzeug und umgebender Luft zu studieren, stellt man umfassende Berechnungen an. Dabei verwendet man eine lokale Darstellung des Impulstransportes in Luft. Diese Impulsbilanz ist unter dem Namen Navier-Stokes-Gleichung bekannt.
Link
- Videovortrag (leicht polemisch)
- Videovortrag auf Youtube