Lösung zu Impulstransport im Rohr: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
==Frage 1== |
==Frage 1== |
||
Die Strömungsgeschwindigkeiten sind durch die [[Kontinuitätsgleichung]] |
Die Strömungsgeschwindigkeiten sind durch die [[Kontinuitätsgleichung]] gegeben |
||
:<math>I_{V1}=I_{V2}\Rightarrow A_1\cdot v_1 = A_2 \cdot v_2</math> |
|||
wobei für die mittlere Geschwindigkeit gilt |
|||
:<math>v = \frac {I_V}{A}</math> |
|||
Also ist |
|||
:<math>v_1 = \frac {I_V}{A_1} = \frac {0.002 m^3/s}{0.000'962 m^2}</math> = 2.08 m/s |
|||
und |
|||
:<math>v_2 = \frac {0.002 m^3/s}{0.000'491 m^2}</math> = 4.07 m/s. |
|||
==Frage 2== |
==Frage 2== |
||
Die Energiebilanz, das [[Gesetz von Bernoulli]], |
Die Energiebilanz, das [[Gesetz von Bernoulli]], |
||
:<math>\left(p_1+\frac{\varrho}{2}v_1^2\right)I_V=\left(p_2+\frac{\varrho}{2}v_2^2\right)I_V</math> |
|||
liefert für den Druck im zweiten Querschnitt |
|||
:<math>p_2 = p_1 + \frac{\rho}{2}(v_1^2 - v_2^2) = 15 kPa + \frac{850 kg/m^3}{2} \left((2.08 m/s)^2 - (4.07 m/s)^2 \right)</math> = 9.80 kPa. |
|||
==Frage 3== |
==Frage 3== |
||
Die Flüssigkeit transportiert den [[Impuls]] [[leitungsartig]] und [[konvektiv]]. Es findet jedoch kein Impulsaustausch mit dem [[Gravitationsfeld]] statt, weil sich der Querschnitt A<sub>1</sub> auf gleicher Höhe wie A<sub>2</sub> befindet. |
|||
[[Bild:Impulstransport im Rohr.png|thumb|Konisches Rohrstück]]Die Flüssigkeit transportiert den [[Impuls]] [[leitungsartig]] und [[konvektiv]], jedoch nicht [[feldartig|feldartig]], gravitativ (Annahme, dass A<sub>1</sub> und A<sub>2</sub> sich auf gleicher Höhe befinden). Man betrachtet die Flüssigkeit im Rohrstück als System. Der Leitungsanteil des Impulsstroms, der durch einen Querschnitt fliesst, besteht aus der Druckkraft, die die aussenliegende Flüssigkeit auf das System ausübt. Sie beträgt hier <math>F_1 = A_1 \cdot p_1 = 0.000'962 m^2 \cdot 15 kPa = 14.43 N </math> und <math>F_2 = A_2 \cdot p_2 = 0.000'491 m^2 \cdot 9.8 kPa = 4.81 N </math>. |
|||
===Querschnitt 1=== |
|||
Stärke des leitungsartigen Impulsstromes |
|||
:<math>I_{p1}=A_1\cdot p_1=0.000'962 m^2 \cdot 15 kPa=14.43 N </math> |
|||
Stärke des konvektiven Impulsstromes |
|||
:<math>I_{px1,konv}=v_{x1}\cdot I_m=\frac{I_V}{A_1}\cdot\rho\cdot I_V=\frac{\rho}{A_1}\cdot I_V ^2=3.53 N</math> |
|||
===Querschnitt 2=== |
|||
Stärke des leitungsartigen Impulsstromes |
|||
:<math>F_2 = A_2 \cdot p_2 = 0.000'491 m^2 \cdot 9.8 kPa = 4.81 N </math> |
|||
Stärke des konvektiven Impulsstromes |
|||
<math>I_{px2,konv}=\frac{\rho}{A_2}\cdot I_V ^2=6.92 N</math> |
|||
===Erhaltungsgrössen=== |
|||
Zählt man beide Stromstärken zusammen, erhält man für die beiden Querschnittsflächen unterschiedliche Impulsstromstärken |
|||
: ''I<sub>px1</sub>'' = 14.43 N + 3.53 N = 18.0 N |
|||
:''I<sub>px2</sub>'' = 4.81 N + 6.92 N = 11.7 N |
|||
Weil sich das Rohr sanft verjüngt, bleibt im Idealfall die von der Flüssigkeit transportierte [[Energie]] längs des Stromes erhalten. Der mitgeführte [[Impuls]] nimmt dagegen ab. Bei einem Rohr, dessen Querschnitt plötzlich zunimmt, ist es umgekehrt. In diesem Fall bleibt der Impuls längs des Flüssigkeitsstromes erhalten und die mittransportierte Energie nimmt ab. |
|||
===Kraftbild=== |
|||
[[Bild:Impulstransport im Rohr.png|thumb|Konisches Rohrstück]]Im Kraftbild betrachtet man die Flüssigkeit im Rohrstück als System ([[freischneiden]]). Der Leitungsanteil des Impulsstroms, der durch einen Querschnitt fliesst, heisst dann Druckkraft der aussen liegenden Flüssigkeit auf das System. Die Kraft ''F<sub>1</sub>'' ist nach rechts und ''F<sub>2</sub>'' nach links gerichtet (um den Übergang vom [[Impulsstrombild]] zum [[freischneiden|Kraftbild]] genau zu verstehen, muss man wissen, dass die [[Referenzfläche]] immer ins Innere des ausgewählten Systems zu orientieren ist). Im Kraftbild dürfen die konvektiven Impulsströme ebenfalls als Kraftpfeile dargestellt werden. Die Grösse des Kraftpfeils ist gleich |
|||
:<math>\vec F=\vec v I_m</math> |
|||
Dabei ist F1 nach rechts und F2 nach links gerichtet. |
|||
Man beachte, dass ein zufliessender Massenstrom positiv und ein abfliessender negativ gezählt wird. |
|||
Der konvektive Anteil ist an den Volumenstrom gekoppelt: <math>I_{px1,konv} = v_{x1} \cdot I_m = \frac {I_V}{A_1} \cdot \rho \cdot I_V = \frac {\rho}{A_1} \cdot I_V ^2 = 3.53 N</math> und <math>I_{px2,konv} = \frac {\rho}{A_2} \cdot I_V ^2 = 6.92 N</math>. Zählt man beide Stromstärken zusammen, erhält man für die beiden Querschnittsflächen unterschiedliche Impulsstromstärken: ''I<sub>px1</sub>'' = 14.43 N + 3.53 N = 18.0 N und ''I<sub>px2</sub>'' = 4.81 N + 6.92 N = 11.7 N. |
|||
==Frage 4== |
|||
Die Differenz der beiden Impulsstromstärken von 6.3 N muss im konisch zulaufenden Teil von der Flüssigkeit an die Rohrwand abgegeben werden. Diese Differenz entspricht der x-Komponente der Kraft F<sub>W</sub>, die die Wand auf die Flüssigkeit ausübt. Weil die Wand rotationssymmetrisch um die x-Achse verläuft, sind die über die ganze Wand aufsummierten Kräfte dF<sub>Wand</sub> gleich einer zur x-Achse parallel ausgerichteten Kraft F<sub>Wand</sub>. |
|||
'''[[Impulstransport im Rohr|Aufgabe]]''' |
'''[[Impulstransport im Rohr|Aufgabe]]''' |
||
Aktuelle Version vom 16. März 2010, 20:03 Uhr
Rohrquerschnitte
- Eingang: [math]A_1 =\pi/4 \cdot(0.035 m)^2 = 0.000'962 m^2, \quad[/math]
- Ausgang: [math]A_2 =\pi /4\cdot(0.025 m)^2 = 0.000'491 m^2[/math]
Frage 1
Die Strömungsgeschwindigkeiten sind durch die Kontinuitätsgleichung gegeben
- [math]I_{V1}=I_{V2}\Rightarrow A_1\cdot v_1 = A_2 \cdot v_2[/math]
wobei für die mittlere Geschwindigkeit gilt
- [math]v = \frac {I_V}{A}[/math]
Also ist
- [math]v_1 = \frac {I_V}{A_1} = \frac {0.002 m^3/s}{0.000'962 m^2}[/math] = 2.08 m/s
und
- [math]v_2 = \frac {0.002 m^3/s}{0.000'491 m^2}[/math] = 4.07 m/s.
Frage 2
Die Energiebilanz, das Gesetz von Bernoulli,
- [math]\left(p_1+\frac{\varrho}{2}v_1^2\right)I_V=\left(p_2+\frac{\varrho}{2}v_2^2\right)I_V[/math]
liefert für den Druck im zweiten Querschnitt
- [math]p_2 = p_1 + \frac{\rho}{2}(v_1^2 - v_2^2) = 15 kPa + \frac{850 kg/m^3}{2} \left((2.08 m/s)^2 - (4.07 m/s)^2 \right)[/math] = 9.80 kPa.
Frage 3
Die Flüssigkeit transportiert den Impuls leitungsartig und konvektiv. Es findet jedoch kein Impulsaustausch mit dem Gravitationsfeld statt, weil sich der Querschnitt A1 auf gleicher Höhe wie A2 befindet.
Querschnitt 1
Stärke des leitungsartigen Impulsstromes
- [math]I_{p1}=A_1\cdot p_1=0.000'962 m^2 \cdot 15 kPa=14.43 N [/math]
Stärke des konvektiven Impulsstromes
- [math]I_{px1,konv}=v_{x1}\cdot I_m=\frac{I_V}{A_1}\cdot\rho\cdot I_V=\frac{\rho}{A_1}\cdot I_V ^2=3.53 N[/math]
Querschnitt 2
Stärke des leitungsartigen Impulsstromes
- [math]F_2 = A_2 \cdot p_2 = 0.000'491 m^2 \cdot 9.8 kPa = 4.81 N [/math]
Stärke des konvektiven Impulsstromes
[math]I_{px2,konv}=\frac{\rho}{A_2}\cdot I_V ^2=6.92 N[/math]
Erhaltungsgrössen
Zählt man beide Stromstärken zusammen, erhält man für die beiden Querschnittsflächen unterschiedliche Impulsstromstärken
- Ipx1 = 14.43 N + 3.53 N = 18.0 N
- Ipx2 = 4.81 N + 6.92 N = 11.7 N
Weil sich das Rohr sanft verjüngt, bleibt im Idealfall die von der Flüssigkeit transportierte Energie längs des Stromes erhalten. Der mitgeführte Impuls nimmt dagegen ab. Bei einem Rohr, dessen Querschnitt plötzlich zunimmt, ist es umgekehrt. In diesem Fall bleibt der Impuls längs des Flüssigkeitsstromes erhalten und die mittransportierte Energie nimmt ab.
Kraftbild
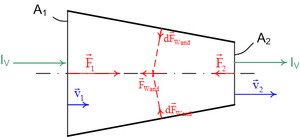
Im Kraftbild betrachtet man die Flüssigkeit im Rohrstück als System (freischneiden). Der Leitungsanteil des Impulsstroms, der durch einen Querschnitt fliesst, heisst dann Druckkraft der aussen liegenden Flüssigkeit auf das System. Die Kraft F1 ist nach rechts und F2 nach links gerichtet (um den Übergang vom Impulsstrombild zum Kraftbild genau zu verstehen, muss man wissen, dass die Referenzfläche immer ins Innere des ausgewählten Systems zu orientieren ist). Im Kraftbild dürfen die konvektiven Impulsströme ebenfalls als Kraftpfeile dargestellt werden. Die Grösse des Kraftpfeils ist gleich
- [math]\vec F=\vec v I_m[/math]
Man beachte, dass ein zufliessender Massenstrom positiv und ein abfliessender negativ gezählt wird.
Frage 4
Die Differenz der beiden Impulsstromstärken von 6.3 N muss im konisch zulaufenden Teil von der Flüssigkeit an die Rohrwand abgegeben werden. Diese Differenz entspricht der x-Komponente der Kraft FW, die die Wand auf die Flüssigkeit ausübt. Weil die Wand rotationssymmetrisch um die x-Achse verläuft, sind die über die ganze Wand aufsummierten Kräfte dFWand gleich einer zur x-Achse parallel ausgerichteten Kraft FWand.