Magnus-Effekt: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
K (Leerschlag bei Gleichungen eingefügt) |
||
| Zeile 10: | Zeile 10: | ||
Für diese Strömungsmodell (Superposition eines Potenzialwirbels mit einer Potenzialströmung) liefert der Satz von Kutta-Zhukhovski die Kraft pro Profillänge (Einheit N/m) |
Für diese Strömungsmodell (Superposition eines Potenzialwirbels mit einer Potenzialströmung) liefert der Satz von Kutta-Zhukhovski die Kraft pro Profillänge (Einheit N/m) |
||
<math>f_A = v_\infty \rho \Gamma</math> |
<math> f_A = v_\infty \rho \Gamma</math> |
||
wobei v<sub>oo</sub> die Anströmgeschwindigkeit bezeichnet und mit ''Γ'' die Zirkulation (Einheit m<sup>2</sup>/s), ein Wegintegral über die Strömungsgeschwindigkeit, gemeint ist |
wobei v<sub>oo</sub> die Anströmgeschwindigkeit bezeichnet und mit ''Γ'' die Zirkulation (Einheit m<sup>2</sup>/s), ein Wegintegral über die Strömungsgeschwindigkeit, gemeint ist |
||
<math>\Gamma = \int \vec v \bullet d\vec s</math> |
<math> \Gamma = \int \vec v \bullet d\vec s</math> |
||
Man darf nun in guter Näherung annehmen, dass die umgebende Luft unmittelbar über dem rotierenden Körper die gleich Gesschwindigkeit besitzt wie die Körperoberfläche. Dann ist die Zirkulation gleich Umfang mal Umgangsgeschwindigkeit bezüglich der Körperachse (die Anströmung trägt als reine Potenzialströmung nichts zur Zirkulation bei) |
Man darf nun in guter Näherung annehmen, dass die umgebende Luft unmittelbar über dem rotierenden Körper die gleich Gesschwindigkeit besitzt wie die Körperoberfläche. Dann ist die Zirkulation gleich Umfang mal Umgangsgeschwindigkeit bezüglich der Körperachse (die Anströmung trägt als reine Potenzialströmung nichts zur Zirkulation bei) |
||
<math>\Gamma = (2 \pi r) (\omega r) = 2 \omega A</math> |
<math> \Gamma = (2 \pi r) (\omega r) = 2 \omega A</math> |
||
wobei mit ''A'' die Querschnittsfläche des den rotierenden Körper gemeint ist. Für die Magnuskraft pro Länge gilt dann |
wobei mit ''A'' die Querschnittsfläche des den rotierenden Körper gemeint ist. Für die Magnuskraft pro Länge gilt dann |
||
<math>f_M = 2 v_\infty \rho \omega A</math> |
<math> f_M = 2 v_\infty \rho \omega A</math> |
||
Weil die Magnuskraft genau senkrecht zur Anströmung steht, kann auch eine Vektordarstellung gegeben werden |
Weil die Magnuskraft genau senkrecht zur Anströmung steht, kann auch eine Vektordarstellung gegeben werden |
||
<math>\vec f_M = 2 \rho (\vec v_\infty \times \vec \omega) A</math> |
<math> \vec f_M = 2 \rho (\vec v_\infty \times \vec \omega) A</math> |
||
Integriert man längs der Rotationsachse auf, erhält man die Magnuskraft auf den entsprechenden Körper. |
Integriert man längs der Rotationsachse auf, erhält man die Magnuskraft auf den entsprechenden Körper. |
||
<math>\vec F_M = 2 \rho_{Luft} (\vec v_\infty \times \vec \omega) V_{Koerper}</math> |
<math> \vec F_M = 2 \rho_{Luft} (\vec v_\infty \times \vec \omega) V_{Koerper}</math> |
||
Diese theoretische Erklärung des Magnuseffekts ist nur auf zylindersymmetrische Körper, die um ihre eigene Symmetrieachse rotieren, anwendbar. Die reibungsbedingte Kraftwirkung parallel zur Anströmung, das reibungsbedingte Drehmoment und der [[statischer Auftrieb]] sind separat zu modellieren. |
Diese theoretische Erklärung des Magnuseffekts ist nur auf zylindersymmetrische Körper, die um ihre eigene Symmetrieachse rotieren, anwendbar. Die reibungsbedingte Kraftwirkung parallel zur Anströmung, das reibungsbedingte Drehmoment und der [[statischer Auftrieb]] sind separat zu modellieren. |
||
Version vom 5. Februar 2008, 10:30 Uhr
Phänomen
Die Flugbahn eines rotierenden Fussballs nimmt einen eigenen Verlauf. Je nach Richtung der Drehachse weicht er seitwärts weg, taucht sehr schnell ab oder scheint förmlich zu schweben. Dieser Effet ermöglicht die direkte Verwertung eines Eckstosses oder das Zuspiel über eine Bananenflanke. Das gleiche Phänomen kann im Tennis, Tischtennis (Topspin, Sidespin) oder Faustball (Seitenschnitt) zur Täuschung des Gegners eingesetzt werden.
Heinrich Gustav Magnus (2. 5. 1802 - 4. 4. 1870) hat dieses Phänomen erstmals wissenschaftlich untersucht, um die Ablenkung von Artilleriegeschossen aus der ballistischen Bahn zu erklären.
Theorie
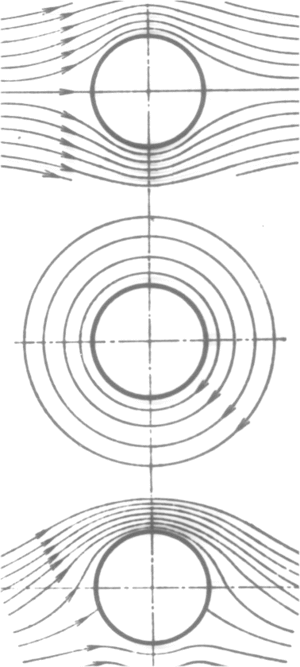
Zur Erklärung des Magnus-Effektes ersetzt man die reale Strömung durch eine reibungsfreie Strömung eines inkompressiblen Fluids. Die reibungsbedingte Wirkung des rotierenden Körpers auf das Fluid geht durch eine Wirbelströmung in dieses Modell ein. Die Strömung um den rotierenden Körper setzt sich demnach aus einer Potenzialströmung und einem Potenzialwirbel zusammen (eine Potenzialströmung ist überall wirbelfrei, d.h. die Winkelgeschwindigkeit ist überall Null; ein Potenzialwirbel ist mit Ausnahme des Zentrums, das nicht zum Strömungsgebiet gehört, überall wirbelfrei). Der dynamische Auftrieb eines Flugzeugflügels wird analog erklärt. Nur wird dort die Wirbelströmung nicht durch einen rotierenden Körper, sondern durch das Zusammenwirken von Wirbelstrasse und Geometrie des umströmten Körpers induziert.
Für diese Strömungsmodell (Superposition eines Potenzialwirbels mit einer Potenzialströmung) liefert der Satz von Kutta-Zhukhovski die Kraft pro Profillänge (Einheit N/m)
[math] f_A = v_\infty \rho \Gamma[/math]
wobei voo die Anströmgeschwindigkeit bezeichnet und mit Γ die Zirkulation (Einheit m2/s), ein Wegintegral über die Strömungsgeschwindigkeit, gemeint ist
[math] \Gamma = \int \vec v \bullet d\vec s[/math]
Man darf nun in guter Näherung annehmen, dass die umgebende Luft unmittelbar über dem rotierenden Körper die gleich Gesschwindigkeit besitzt wie die Körperoberfläche. Dann ist die Zirkulation gleich Umfang mal Umgangsgeschwindigkeit bezüglich der Körperachse (die Anströmung trägt als reine Potenzialströmung nichts zur Zirkulation bei)
[math] \Gamma = (2 \pi r) (\omega r) = 2 \omega A[/math]
wobei mit A die Querschnittsfläche des den rotierenden Körper gemeint ist. Für die Magnuskraft pro Länge gilt dann
[math] f_M = 2 v_\infty \rho \omega A[/math]
Weil die Magnuskraft genau senkrecht zur Anströmung steht, kann auch eine Vektordarstellung gegeben werden
[math] \vec f_M = 2 \rho (\vec v_\infty \times \vec \omega) A[/math]
Integriert man längs der Rotationsachse auf, erhält man die Magnuskraft auf den entsprechenden Körper.
[math] \vec F_M = 2 \rho_{Luft} (\vec v_\infty \times \vec \omega) V_{Koerper}[/math]
Diese theoretische Erklärung des Magnuseffekts ist nur auf zylindersymmetrische Körper, die um ihre eigene Symmetrieachse rotieren, anwendbar. Die reibungsbedingte Kraftwirkung parallel zur Anströmung, das reibungsbedingte Drehmoment und der statischer Auftrieb sind separat zu modellieren.