Thermodynamik

Gebiet

Die Thermodynamik beschäftigt sich mit der Dynamik (Speicher- und Transportvorgänge) der Entropie und der damit verbundenen Erwärmung und Ausdehnung von Körpern. Unter einem Körper verstehen wir hier eine abgrenzbare Menge "Materie" mit Masse, Volumen, Energie- und Entropiespeichervermögen. Der Entropiegehalt eines homogenen Körpers ist durch seine Temperatur und sein Volumen eindeutig beschrieben. Inhomogene Körper können durch Temperatur- und Dichteverteilung charakterisiert werden.

Modellmässig kann man die Körper in Speicher- und Stromelemente unterteilen. Obwohl jeder Körper gleichzeitig Entropie speichert und weiterleitet, macht diese Einteilung Sinn. Betrachten wir dazu ein Gefäss mit heissem Wasser, das sich gegen die Umgebung abkühlt. In einer ersten Beschreibung modelliert man das Wasser als Speicher, die Gefässwand, die Grenzschicht der Luft sowie den strahlungsartigen Entropietransport an die Umgebung als Stromelemente. Dieses Grobmodell lässt sich später verfeinern, indem zum Beispiel der Gefässwand auch noch eine Speicherfähigkeit zugesprochen wird.

Bei der Wärmeleitung und der Wärmestrahlung wird Entropie erzeugt. Folglich muss in jedem Stromelement noch die Entropieproduktionsrate berechnet und dem am Ausgang wegfliessenden Entropiestrom zugeschlagen werden. Diese etwas umständliche Modellierung lässt sich vermeiden, wenn man statt der Entropie die Energie als bilanzierfähige Grösse nimmt. Diese Alternative, statt der Entropie die Energie (statt der Primärgrösse die Begleitgrösse) zu bilanzieren , bringt aber nur bei total irreversiblen Prozessen wie Mischvorgängen oder Wärmeleitung eine Vereinfachung. Bei den wirklich interessanten Prozessen, wie sie in Wärmekraftmaschinen, Wärmepumpen oder Lebewesen ablaufen, kommt man um die Entropiebilanz nicht mehr herum.

Struktur

Bilanz

Ein Körper kann über die Oberfläche mit einem benachbarten Körper oder mittels Quellen über das elektromagnetische Feld Entropie austauschen. Die Entropiebilanz besagt, dass die Summe über alle Entropiestromstärken und die Entropiequellenstärke sowie die Entropieproduktionsrate gleich der Entropieänderungsrate ist. Zufliessende Ströme, Quellen und Entropieproduktion gehen mit einem positiven Vorzeichen, abfliessende Ströme und Senken mit einem negativen Vorzeichen in die Bilanz ein.

Offene Systeme tauschen zusätzlich Entropie mittels konvektiven Strömen aus. Konvektive Ströme produzieren im Innern des Systems durch Mischvorgänge meist noch zusätzliche Entropie.

konstitutive Gesetze

Wärmespeicher werden in der Regel bei konstant gehaltenem Druck (isobar) betrieben. Das Verhalten homogener Wärmespeicher wird mittels spezifischer Grössen beschrieben. Oft sind aber nur die Werte bezüglich der Energie (innere Energie bei konstantem Volumen und Enthalpie bei konstanten Druck) tabelliert. Die Umrechnung von den energetischen (enthalpischen) in die entropischen Grössen erfolgt, wie mit Hilfe der Energie- und Entropiebilanz sowie des zugeordneten Energiestromes gezeigt werden kann, durch Division mit der absolute Temperatur.

spezifische Enthalpie und Entropie

Grösse	Formelzeichen	Einheit	Wert
spezifische Wärmekapazität	c	J/(K kg)	tabelliert
spezifische Schmelzenthalpie	q	J/kg	tabelliert
spezifische Verdampfungsenthalpie	r	J/kg	tabelliert
spezifische Entropiekapazität	cS	J/(K2 kg)	c/T
spezifische Schmelzentropie	qS	J/(K kg)	q/T
spezifische Verdampfungsentropie	rS	J/(K kg)	r/T

Wärme ist die Energie, die zusammen mit der Entropie über die Systemgrenze transportiert wird. Folglich hat das Wort Wärme bei Speichereigenschaften nichts zu suchen. Dass in den Tabellenbüchern die Schmelz- und Verdampfungsenthalpien oft mit Schmelz- und Verdampfungswärmen und die Enthalpieänderung pro Temperatur mit Wärmekapazität bezeichnet wird, zeigt, wie inkonsistent die Themodynamik gehandhabt wird.

Die Wärmeleitung in homogenen Stoffen wird von der Wärmeleitfähigkeit bestimmt. Diese Grösse beschreibt die Fähigkeit eines Stoffes, "Wärme" zu transportieren. Weil bei der Wärmeleitung die Energie erhalten bleibt und die Entropie maximal zunimmt, ist die Wärmeleitfähigkeit bezüglich der Erhaltungsgrösse Energie definiert. Die Wärmeleitfähigkeit beschreibt den Zusammenhang zwischen dem Temperaturgefälle und der Energiestromdichte.

Die Beschreibung des strahlungsartige Entropietransportes basiert auf dem Modell der Hohlraumstrahlung.

Ändert ein homogenes System sowohl den Druck als auch die Temperatur, sind die beiden Potenzialgrössen Temperatur und Druck mit den beiden Primärgrössen Entropie und Volumen verknüpft. Das einfachste Modell für einen dermassen gekoppelten Speicher ist das ideale Gas

Rolle der Energie

Ein Entropiestrom ist immer von einem Energiestrom begleitet. Die Temperatur der Referenzfläche ordnet der Entropiestromstärke eine Energiestromstärke zu

Energiestromstärke = absolute Temperatur mal Entropiestromstärke

Die Temperatur ist das Energiebeladungsmass des Entropiestromes. Ändert sich die Temperatur längs des Entropiestromes, wird eine Prozessleistung umgesetzt

Prozessleistung = Temperaturdifferenz mal Entropiestromstärke

Bei der Wärmeleitung wird mit der freigesetzten Prozessleistung zusätzlich Entropie produziert. Dies führt dazu, dass im stationären Prozess der Energiestrom am Ausgang des wärmeleitenden Elementes gleich stark wie beim Eingang ist, der Entropiestrom dafür maximal zunimmt. Bei einer idealen Wärmepumpe oder Wärmekraftmaschine ist es gerade umgekehrt. Bei diesen Geräten fliesst der Entropiestrom unverändert durch und der zugeordnete Energiestrom nimmt maximal zu oder ab.

Homogene Speicher können aufgrund ihrer Modellstruktur keine Entropie produzieren. Folglich spielt es keine Rolle, ob die Energie oder die Entropie bilanziert wird. Der Zusammenhang zwischen diesen beiden Grössen wird über den zugeordneten Energiestrom hergestellt.

Solange sich ein System maximal irreversibel verhält, ist es über die Energie einfacher als über die Entropie zu modellieren. Mit der energetischen Modellierungsmethode können Vorgänge wie Auskühlung eines Hauses oder Mischen von warmen und kaltem Wasser einfach beschrieben werden.

Beispiel

Kernkraftwerk mit Druckwasserreaktor

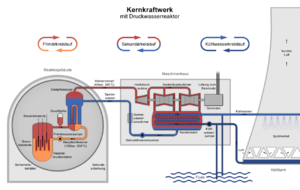
Zu einem Kernkraftwerk mit Druckwasserreaktor liegen folgende Daten vor:

Reaktorleistung:	3765 MW
Generatorleistung:	1395 MW
Temperatur im Dampferzeuger:	287°C
Temperatur im Kondensator:	47°C

Wie gross ist die Entropieproduktionsrate im Sekundärkreis?

Wenn wir annehmen, dass keine Wärme über das Gebäude weggeht, kann der über die Kühlung wegfliessende Energiestrom als Differenz aus Reaktorleistung und Generatorleistung berechnet werden. Die Kühlleistung beträgt demnach 2370 MW. Mit Hilfe des Konzepts des zugeordneten Energiestromes können nun die Entropieströme am Eingang (6.723 MW/K) und am Ausgang (7406 MW/K) des Sekundärkreises berechnet werden. Die Entropieproduktionsrate beträgt folglich 683 kW/K. Im Sekundärkreis vermehrt sich die zugeführte Entropie also um etwa 10%. Dies stellt das theoretische Verbesserungspotenzial dieser Anlage dar.

Wer in diesem Beispiel nur die Energiebilanz verwendet und dann noch meint, Energie sei Arbeitsvermögen, kommt zum Schluss, dass in einem Kernkraftwerk gewaltige Energiemengen verschwendet werden. Erst die Entropiebetrachtung liefert hier das korrekte Bild eines Wasserfalles: Entropie wird im Reaktor bei der technisch zulässigen Höchsttemperatur produziert und über die Turbinen an die Umwelt abgeführt. Als Arbeitsvermögen steht nur die Prozessleistung zwischen der Temperatur des Reaktors und der Umgebungstemperatur zur Verfügung.

Links

• E-Learning-Kurs zur Thermodynamik