Lösung zu Güterwagen beladen: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
K (Skizze) |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Bild:Gueterwagen_beladen.png]] |
[[Bild:Gueterwagen_beladen.png]] |
||
Der Massenstrom beträgt: I<sub>m</sub> = 24 t / 12 s = 2000 kg/s, die Gesamtmasse m = 15'000 kg + 2000 kg/s * t. |
|||
Die [[Impulsbilanz]] für den Wagen plus geladenes Schüttgut (Masse m für beides) in vertikaler Richtung lautet: |
Die [[Impulsbilanz]] für den Wagen plus geladenes Schüttgut (Masse m für beides) in vertikaler Richtung lautet: |
||
| Zeile 6: | Zeile 8: | ||
:<math>{-}F_N + m \cdot g + v_{Sy} \cdot I_m = 0</math> |
:<math>{-}F_N + m \cdot g + v_{Sy} \cdot I_m = 0</math> |
||
Die [[Normalkraft]] steigt kontinuierlich von 167 |
Die [[Normalkraft]] F<sub>N</sub> = (15'000 kg + 2000 kg/s * t) * 9.81 m/s2 + 10 m/s * 2000 kg/s = 167 kN + 19.6 kN/s * t steigt kontinuierlich von 167 kN auf 402 kN an. |
||
In horizontaler Richtung lautet die Impulsbilanz : |
In horizontaler Richtung lautet die Impulsbilanz : |
||
:<math>F_Z - F_R + v_{Sx} \cdot I_m = m \dot v_{Wx} + \dot m v_{Wx}</math> |
:<math>F_Z - F_R + v_{Sx} \cdot I_m = \dot {(m v_{Wx})} = m \dot v_{Wx} + \dot m v_{Wx}</math> |
||
Die Beschleungigung des Wagens und die Horizontalgeschwindigkeit v<sub>Sx</sub> des auftreffenden Schüttgutes sind gleich Null. Deshalb gilt |
Die Beschleungigung des Wagens <math> \dot v_{Wx} </math>und die Horizontalgeschwindigkeit v<sub>Sx</sub> des auftreffenden Schüttgutes sind gleich Null. Deshalb gilt |
||
:<math>F_Z - F_R = \dot m v_{Wx}</math> |
:<math>F_Z - F_R = \dot m v_{Wx}</math> |
||
| Zeile 18: | Zeile 20: | ||
oder umgeformt (die Änderungsrate ist gleich der Stromstärke der zufliessenden Masse) |
oder umgeformt (die Änderungsrate ist gleich der Stromstärke der zufliessenden Masse) |
||
:<math>F_Z = \mu F_N + I_m \cdot v_{Wx}</math> |
:<math>F_Z = \mu F_N + I_m \cdot v_{Wx}</math> = 0.04 * (167 kN + 19.6 kN/s * t) + 2'000 kg/s * 1 m/s = 8.68 kN + 0.784 kN/s * t |
||
Die Zugkraft ''F<sub>Z</sub>'' steigt kontinuierlich von 8. |
Die Zugkraft ''F<sub>Z</sub>'' steigt kontinuierlich von 8.68 kN auf 18.1 kN an. |
||
'''[[Güterwagen beladen|Aufgabe]]''' |
'''[[Güterwagen beladen|Aufgabe]]''' |
||
Aktuelle Version vom 23. Februar 2010, 10:50 Uhr
Der Massenstrom beträgt: Im = 24 t / 12 s = 2000 kg/s, die Gesamtmasse m = 15'000 kg + 2000 kg/s * t.
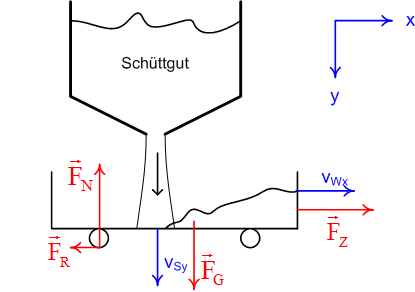
Die Impulsbilanz für den Wagen plus geladenes Schüttgut (Masse m für beides) in vertikaler Richtung lautet:
- [math]{-}F_N + m \cdot g + v_{Sy} \cdot I_m = 0[/math]
Die Normalkraft FN = (15'000 kg + 2000 kg/s * t) * 9.81 m/s2 + 10 m/s * 2000 kg/s = 167 kN + 19.6 kN/s * t steigt kontinuierlich von 167 kN auf 402 kN an.
In horizontaler Richtung lautet die Impulsbilanz :
- [math]F_Z - F_R + v_{Sx} \cdot I_m = \dot {(m v_{Wx})} = m \dot v_{Wx} + \dot m v_{Wx}[/math]
Die Beschleungigung des Wagens [math] \dot v_{Wx} [/math]und die Horizontalgeschwindigkeit vSx des auftreffenden Schüttgutes sind gleich Null. Deshalb gilt
- [math]F_Z - F_R = \dot m v_{Wx}[/math]
oder umgeformt (die Änderungsrate ist gleich der Stromstärke der zufliessenden Masse)
- [math]F_Z = \mu F_N + I_m \cdot v_{Wx}[/math] = 0.04 * (167 kN + 19.6 kN/s * t) + 2'000 kg/s * 1 m/s = 8.68 kN + 0.784 kN/s * t
Die Zugkraft FZ steigt kontinuierlich von 8.68 kN auf 18.1 kN an.