Aviatik 2009/3: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
|||
| Zeile 54: | Zeile 54: | ||
'''[[Lösung zu Aviatik 2009/3|Lösung]]''' |
'''[[Lösung zu Aviatik 2009/3|Lösung]]''' |
||
'''[https://cast.switch.ch/vod/clips/20lwicrg4f/link_box Lösungsvideo]''' |
|||
[[Kategorie:Pruefungen]] |
[[Kategorie:Pruefungen]] |
||
Aktuelle Version vom 2. Juli 2010, 19:12 Uhr
Studiengang Aviatik der ZHAW
Erlaubte Hilfsmittel: Taschenrechner, selbstverfasste Formelsammlung
Daten:
- Gravitationsfeldstärke = 9.81 N/kg
- Dichte von Wasser = 1000 kg/m3
- spezifische Wärmekapazität von Wasser = 4.19 kJ/(kg*K)
- spezifische Schmelzenthalpie von Wasser = 334 kJ/kg
- universelle Gaskonstante R = 8.31 J/(mol*K)
- molare Energiekapazität von Luft = 5/2*R
- molare Enthalpiekapazität von Luft = 7/2*R
Aufgabe 1
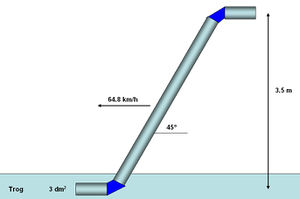
Der „Flying Scotsman“ ist ein Zug, der zwischen London und Edinburgh verkehrt. Damit die Strecke schon in den dreissiger Jahren ohne Zwischenhalt befahren werden konnte, rüstete man die Dampfloks mit Schöpfrohren (Skizze) aus. Mit diesen Schöpfrohren konnten die Loks während der Fahrt Wasser aus Trögen entnehmen, die zwischen den Schienen lagen. Eine Lok, die mit 64.8 km/h fährt, benötigt eine Strecke (minimale Länge des Trogs) von 540 m, um 9'000 Liter Wasser über ein Schöpfrohr mit einem offenen Querschnitt 3 dm2 aufzunehmen.
- Mit welcher Geschwindigkeit strömt das Wasser durch das Schöpfrohr?
- Welche Leistung (Prozessleistung) muss zugeführt werden, um diesen Wasserstrom aus dem Trog auf die geforderte Geschwindigkeit zu beschleunigen?
- Mit welcher zusätzlichen Kraft muss das untere Ende des Schöpfrohres festgehalten werden, weil das Wasser dort um 45° umgelenkt wird? In welche Richtung muss diese Kraft wirken?
- Mit welcher Geschwindigkeit würde das Wasser durch das Schöpfrohr fliessen, wenn keine Reibung vorhanden wäre und das Wasser um 3.5 Meter angehoben werden muss?
Hinweis: Wählen Sie für die Teilaufgaben a) c) und d) den fahrenden Zug als Bezugssystem.
Aufgabe 2
In einer Freizeitanlage wird mit Hilfe einer Wärmepumpe Eis aus Wasser der Temperatur 15°C hergestellt. Die Abwärme dient dazu, das Wasser für das Hallenbad von 15°C auf 28°C aufzuheizen.
- Wie viel Energie und wie viel Entropie muss man einem Kilogramm Wasser von 15°C entziehen, damit es in Eis von 0° umgewandelt wird?
- Eine Wärmepumpe fördere die vom Eis abgegebene „Wärme“ reversibel von -13°C auf eine Temperatur von 43°C. Wie viel Energie muss der Wärmepumpe zugeführt werden, damit ein Kilogramm Eis produziert wird?
- Wie viele Kilogramm Wasser kann man mit der Abwärme der Pumpe von 15°C auf 28°C erwärmen?
- Wie viel Energie müsste man aufwenden, um 1 Kilogramm Wasser von 15°C absolut reversibel in Eis von 0° C umzuwandeln, wenn die Entropie bei einer Temperatur von 27°C an die Umwelt abgegeben werden kann?
Aufgabe 3
Der Kreisprozess, den die Luft bei einem Strahltriebwerk durchläuft, kann durch vier ideale Teilprozesse näherungsweise beschrieben werden: isentrope Kompression, isobares Heizen, isentrope Expansion bis auf den Anfangsdruck, isobares Auskühlen in der Atmosphäre.
- Skizzieren Sie für diesen Kreisprozess das qualitative T-S- und p-V-Diagramm für ein Mol Luft (zweiatomiges Gas).
- Bei der isentropen Kompression wird der Druck von 0.25 bar auf 10 bar erhöht. Welche Temperatur weist die anfänglich -53°C kalte Luft nach der Kompression auf?
- In der Brennkammer wird die Luft auf 1227°C erwärmt. Wie viel thermische Energie und wie viel Entropie werden einem Mol Luft durch die Verbrennung zugeführt?
- Auf welchen Wert sinkt die Temperatur der Luft bei der isentropen Expansion? Wie viel Wärmeenergie kann die Luft danach noch an die Umgebung abgeben?
Aufgabe 4
Ein Heliumballon hat unmittelbar nach dem Füllen ein Volumen von 5 Litern, eine Temperatur von 20°C und einen Überdruck von 0.1 bar. Danach wird er durch die Sonne aufgeheizt. Der Hauptanteil des auftreffenden Energiestroms heizt die Gummihülle des Ballons auf. Nur ein konstanter Rest von 1 W wird an das Helium abgegeben.
- Skizzieren Sie als erstes das Systemdiagramm (hier noch keine Formeln angeben) des Carnotors (flowchart) mit Entropiebilanz, Volumenbilanz der Hilfsflüssigkeit, zugehörige Potenziale und Energieebene. Lassen Sie den Entropie- und den Volumenstrom vorläufig unabhängig von anderen Grössen.
- Wie wird der Druck des Heliums berechnet (die Berechnung der Temperatur sei schon gegeben)?
- Bauen Sie die Wirkung der Sonne ins Modell ein, inkl. Formel.
- Vervollständigen Sie das Modell, indem Sie die Volumenänderung mit einbeziehen, inkl. Formel.
Hinweise:
- Der Zusammenhang zwischen Druck der Gummihülle und Volumen des Heliums wird wie folgt vereinfacht: [math]p_{Ballon}=p_0+1\frac{bar}{m^3}*(V-V_0)[/math] mit p0 und V0 als Startwerte
- Modellieren Sie den Volumenstrom der Hilfsflüssigkeit mit einem Volumenleitwert von 1 * 10-6 m3/(s*Pa)
- Daten der Umgebung: Druck 1 bar, Temperatur 20°C.
Aufgabe 5
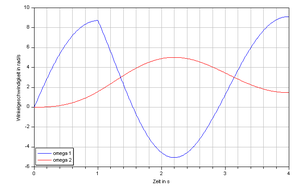
Auf das anfänglich ruhende Schwungrad 1 (Trägheitsmoment 20 kgm2) wirkt während der ersten Sekunde ein konstantes Drehmoment (Antrieb) ein. Über ein Feder-Dämpfer-System ist dieses Rad mit dem Rad 2 (Trägheitsmoment 80 kgm2) verbunden. Beide Räder drehen sich reibungsfrei auf einer gemeinsamen Achse (siehe Diagramm).
- Wie gross ist das Antriebs-Drehmoment, das in der ersten Sekunde auf das erste Schwungrad einwirkt?
- Wie viel Energie wird dem ersten Schwungrad durch den Antrieb zugeführt, d.h. wie gross ist die Arbeit des Drehmoments?
- Welche Prozessleistung setzt der Drehimpulsstrom im Feder-Dämpfer-System zum Zeitpunkt 1.6 s um?
- Wie schnell drehen sich die Räder nach langer Zeit und wie viel Energie ist dann im Feder-Dämpfer-System dissipiert worden?