Enthalpie: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Die Enthalpie (gr. ''en'' = "innerhalb" + ''thalpos'' = "Wärme") ist |
Die Enthalpie (gr. ''en'' = "innerhalb" + ''thalpos'' = "Wärme") ist definiert als innere Energie plus das Produkt aus Druck und Volumen eines homogenen Systems. Die Enthalpie wird somit wie die Energie in Joule (J) gemessen. Als Formelzeichen verwendet man häufig ''H''. Heizt man einen Stoff bei konstantem Druck, entspricht die zugeführte Energie, die Wärme, der Änderung der Enthalpie. Dies erklärt den Namen. |
||
==Motivation== |
==Motivation== |
||
Version vom 20. April 2011, 06:13 Uhr
Die Enthalpie (gr. en = "innerhalb" + thalpos = "Wärme") ist definiert als innere Energie plus das Produkt aus Druck und Volumen eines homogenen Systems. Die Enthalpie wird somit wie die Energie in Joule (J) gemessen. Als Formelzeichen verwendet man häufig H. Heizt man einen Stoff bei konstantem Druck, entspricht die zugeführte Energie, die Wärme, der Änderung der Enthalpie. Dies erklärt den Namen.
Motivation
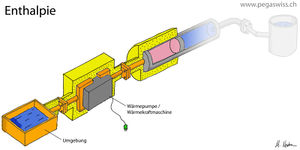
Das Bild zeigt den aktiv beheizten Carnotor, dessen hydraulischer Port mit einem Druckbehälter kurz geschlossen ist. Sucht man nun nach einer Grösse, die aus den Zuständen des im Carnotor enthaltenen Stoffes berechnet werden kann und gleich der Änderung der thermischen Energie (auch Wärme genannt) ist, stösst man auf die Enthalpie.
Heizt man ein Gas oder eine Flüssigkeit auf, kann aus der Energiebilanz (früher 1. Hauptsatz der Thermodynamik genannt)
- [math]I_{W_{therm}}+I_{W_{mech}}=\dot W[/math]
unter Berücksichtigung der Homogenität (überall gleicher Zustand) und der Isotropie (keine Scherspannungen) der mechanische Energiestrom mit Hilfe der Zustandsgrössen Druck und Volumen umgeformt werden
- [math]I_{W_{therm}}=\dot W-I_{W_{mech}}=\dot W+p\dot V[/math]
Die rechte Seite der umgeformten Energiebilanz (Änderungsrate der inneren Energie plus Druck mal Volumenänderungsrate) darf unter der Bedingung, dass der Druck konstant gehalten wird, als Speicher für die thermische Energie aufgefasst werden.
Definition
Die Enthalpie, die der Fiktion des thermischen Energiespeichers entspringt, hat als sauber definierte Zustandsgrösse den Irrtum ihrer Entstehung überlebt. Für homogene Flüssigkeiten und Gase ist die Enthalpie gleich der inneren Energie plus das Produkt aus Volumen und Druck
- [math]H=W+pV[/math] oder in alter Schreibweise [math]H=U + pV[/math]
In der zweiten Form ist das klassische Formelzeichen U für die innere Energie verwendet worden. Die innere Energie oder Selbstenergie eines Systems, die gemäss der Relativtitätstheorie gleich Mass mal Lichtgeschwindigkeit im Quadrat ist, wird üblicherweise bei einem bestimmten Zustand (S0, V0) gleich Null gesetzt.
Heizt man ein homogenes Fluid bei konstantem Druck auf, gilt
- [math]I_{W_{therm}} = \dot W + p \dot V = \dot H[/math]
Bei konstant gehaltenem Druck ist der thermische Energiestrom gleich der Änderungsrate der Enthalpie. Deshalb wird die Enthalpie, die der thermisch ausgetauschten Energie entspricht, oft als Wärmeinhalt gedeutet. Man beachte, dass diese naive Interpretation der Energiebilanz nur gültig ist, solange der Druck konstant gehalten wird.
Die freie Energie, die für die mechanisch gespeicherte Energie steht, übernimmt eine zur Enthalpie äquivalente Funktion. Nur steht dort die Arbeit statt der Wärme im Zentrum des Interesses. Die Enthalpie ist ein Mass für die thermisch gespeicherte Energie, solange die Umwelt den Druck stabilisiert. Die freie Energie ist ein Mass für die mechanisch gespeicherte Energie, solange die Umwelt die Temperatur konstant hält.
einfache, homogene Systeme
Flüssige, gasförmige und auch feste Stoffe bei nicht zu tiefer Temperatur besitzen eine nahezu konstante Wärmekapazität. Heizt man einen solchen Stoff bei konstantem Druck auf, steigt die Temperatur proportional mit der zugeführten Wärmeenergie an
- [math]I_{W_{therm}} = \dot H = m c \dot T = n \hat c \dot T[/math]
Die Wärmkapazazität, die eigentlich Enthalpiekapaztität heissen müsste, wird hier einmal auf die Masse (spezifisch) und einmal auf die Stoffmenge (molar) bezogen.
Nimmt man die Schmelzenthalpie (m q) und die Verdampfungsenthalpie (m r) dazu, kann die Enthalpie eines einfachen, homogenen Systems bei einem gegebenen Druck in Form einer Funktion angegeben werden
- [math]H = H_0 + m \left(c_{fest}(T_{schmelz} - T_0) + q + c_{fluessig}(T_{siede} - T_{schmelz}) + r + c_{gas}(T - T_{siede}) \right)[/math]
Liegt die Temperatur unter dem Siedepunkt für den gegebenen Druck, entfallen einzelne Terme. Liegt ein Gemisch fest/flüssig oder flüssig/gasförmig vor, muss der schon verflüssigte oder vergaste Teil mit der Schmelz- oder Verdampfungsenthalpie multipliziert werden.
Reaktionsenthalpie
Die Reaktionsenthalpie gibt den Energieumsatz einer bei konstantem Druck durchgeführten Reaktion an. Die Reaktionsenthalpie, die mit einem Reaktionskalorimeter gemessen wird, entspricht der Enthalpieänderung des Kalorimeters.
Eine Reaktion kann exotherm oder endotherm verlaufen. Bei einer exothermen Reaktion ist die Enthalpieänderung positiv, d.h. die Reaktanden geben Energie in Form von Wärme an das Kalorimeter ab. Bei einer endothermen nehmen die Stoffe bei der Reaktion Wärme vom Kalorimeter auf. Endotherme Reaktionen hat man erst mit Hilfe einer korrekten Entropiebilanz richtig verstanden. Weil bei jedem irreversiblen, also spontan ablaufenden Prozess Entropie erzeugt wird, hat man zuerst angenommen, dass immer Wärme abgeführt werden muss. Speichern die Edukte aber bei gleichem Druck und fast gleicher Temperatur bedeutend mehr Entropie als die Edukte, kann der zusätzliche Bedarf nicht alleine durch die bei der Reaktion produzierten Entropie gedeckt werden. Folglich muss zusätzlich noch Entropie zugeführt werden. Die zugeführte Entropie mal die absolute Temperatur ergibt die zugeordnete Energie, also die Wärmeenergie. Eine bekannte endotherme Reaktion ist das Lösen von Salzen in Wasser.
natürliche Variablen
Homogene Stoffe können ihre Energie in Form von Wärme oder Arbeit mit der Umgebung austauschen. Wie mit Hilfe des Carnotors gezeigt werden kann, ist die Änderung der Energie einmal direkt mit der Änderung der Entropie und einmal direkt mit der Volumenänderung verbunden. Entropie und Volumen werden deshalb auch als natürliche Variablen der inneren Energie bezeichnet. Ausgedrückt durch Änderungsraten lautet die Verknüpfung wie folgt
- [math]\dot W=T\dot S-p\dot V[/math]
Kombiniert man diese Zuordnung mit der Änderungsrate der Enthalpie gewinnt man eine Darstellung der Enthalpie in ihren natürlichen Variablen, der Entropie und dem Druck
- [math]\dot H=\dot W+\dot p V+p\dot V=T\dot S+V\dot p[/math]
Bezüglich der Enthalpie sind Entropie und Druck als freie Variablen und Temperatur und Volumen als "Potenzialgrössen" anzusehen. Eine entsprechende Interpretation mit Bilanzgrösse und Energiebeladungsmass macht dagegen wenig Sinn.
p-V-Diagramm
Die einem homogenen, isotropen System mechanische zugeführte Energie ist gleich der Fläche unter der Kurve im Druck-Volumen-Diagramm
- [math]W(S_0,V_2)-W(S_0,V_1)=-\int_{V_1}^{V_2}pdV[/math]
Die Änderung der Enthalpie ist gemäss der oben ausgeführten Umformung (unter natürliche Variablen) gleich
- [math]H(S_0,V_2)-H(S_0,V_1)=\int_{p_1}^{p_2}Vdp[/math]
also gleich der Fläche unter der Kurve im Volumen-Druck-Diagramm. Zeichnet man beide Flächen im p-V-Diagramm ein, wird der Zusammenhang zwischen der Energie- und der Enthalpieänderung bei konstant gehaltener Entropie sichtbar. Die Schnittmenge der beiden Flächen ist gleich
- [math]\int_{p_1}^{p_2}Vdp-V_2(p_2-p_1)=-\int_{V_1}^{V_2}pdV-p_1(V_1-V_2)[/math]
Durch geeignete Umformung erhält man wiederum den Zusammenhang zwischen den Änderungen der Enthalpie und der inneren Energie
- [math]\Delta H=\int_{p_1}^{p_2}Vdp=p_2V_2-p_1V_1-\int_{V_1}^{V_2}pdV=p_2V_2-p_1V_1+\Delta W[/math]
Mathematisch betrachtet handelt es sich beim Übergang von der Energie mit den Variablen Entropie und Volumen zur Enthalpie mit den Variablen Entropie und Druck um eine Legendre-Transformation.