Lösung zu Badewanne
- Die zuzuführende Wärmeenergie ist gleich der Änderung der Enthalpie des Wassers [math]\Delta H = m c \Delta T[/math] = 180 kg * 4.19kJ/(kgK) * 25 K = 18.86 MJ. Das sind 5.2 kWh elektrische Energie, 0.46 Liter Heizöl oder 0.0028 Ster Holz.
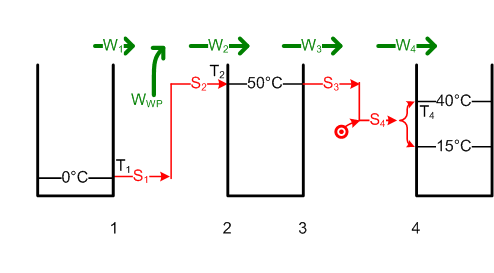
- Weil W3 = W4 = ΔH ist, ist die von der Wärmepumpe bei 50°C abegebene Entropie S3 gleich [math]S_3 = \frac {W_3}{T_2} = \frac {\Delta H}{T_2}[/math] = 58.4 kJ/K. Um die Entropie S1 = S2 = S3 um 50 K hinauf zu pumpen, benötigt die Wärmepumpe die Energie WWP im Umfang von [math]W_{WP} = (T_2 - T_1) \cdot S_1[/math] = 2.9 MJ oder 0.81 kWh.
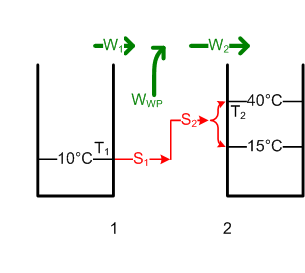
- Die Entropie des Badewassers nimmt um [math]\Delta S = m c \ln{\frac{T_{2e}}{T_{2a}}}[/math] = 62.8 kJ/K zu. Die ausgetauschte Entropiemenge S2, welche diese Entropiezunahme ΔS bewirkte, ist gleich S1. Diese trägt eine Wärmeenergie von [math]W_1 = T_1 S_1[/math] = 17.77 MJ aus dem Grundwasser in die Wärmepumpe hinein. Die Pumpe muss dann noch die Differenz zu W2 aufbringen. Deshalb wird WWP = W2 - W1 = ΔH - W1 = 1.09 MJ (0.3 kWh).
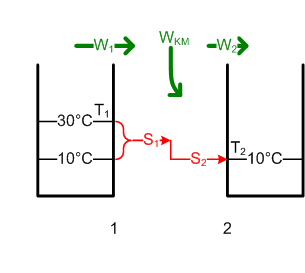
- Die Enthalpie des Badewassers ändert sich um [math]\Delta H = m c \Delta T[/math] = -15.1 MJ und die Entropie um [math]\Delta S = m c \ln{\frac{T_{1e}}{T_{1a}}}[/math] = -51.5 kJ/K. Die ausgetauschte Entropie S1 ist gleich dieser Entropieänderung. Weil reversibel, ist S1 = S2. S2 trägt [math]W2 = T_2 \cdot S_2 = T_2 \cdot \Delta S[/math] = 14.6 MJ als thermische Energie in die Umwelt. Die Differenz WKM zwischen der Enthalpieabnahme ΔH = W1 und der Abwärme W2 ist nutzbar. Eine Wärmekraftmaschine könnte also höchstens 0.5 MJ oder 0.14 kWh Energie zurückgewinnen. Also darf man den Stöpsel beruhigt herausziehen (bei 30°C ist das Baden auch nicht mehr so angenehm).