Aviatik 2012/2
Studiengang Aviatik der ZHAW
Erlaubte Hilfsmittel: Taschenrechner, selbst verfasste Formel- und Beispielsammlung ohne Übungsaufgaben, Wörterbuch für fremdsprachige Studierende. Zusätzlich zu Ihrer Zusammenfassung dürfen Sie zu dieser Prüfung auch eine Protokollseite (A4) pro Experiment des Modellierkurses und des Praktikums (maximal 6 A4-Seiten) mitnehmen. Diese dürfen die physikalische Analyse mit Variablen und Gesetzen, sowie das Flowchart inklusive Formeln enthalten.
Daten:
- Gravitationsfeldstärke = 9.81 N/kg
- Umgebungsdruck = 100 kPa
- Dichte von Wasser = 1000 kg/m3
- spezifische Enthalpiekapazität von Wasser = 419 kJ/(kg*K)
- Universelle Gaskonstante R = 831 J/(mol*K)
- Molare Energie- und Energiekapazität von Luft = 5/2 R; 7/2 R
- Isentropenexponent = 1.4
Aufgabe 1
4 Liter Wasser sollen auf 3 verschiedene Arten von 15°C auf 40°C aufgeheizt werden.
- Wie viel thermische Energie muss ein Tauchsieder ans Wasser abgeben? Wie gross ist dabei die Entropiezunahme im Wasser?
- Wie viel Prozessenergie muss einer Wärmepumpe zugeführt werden, die reversibel zwischen 10°C und 50°C arbeitet?
- Berechnen Sie die im Fall b) produzierte Entropie.
- Wie viel Energie muss mindestens aufgewendet werden, wenn man die Entropie einem Reservoir von 10°C entnimmt (absolut reversible Prozessführung)?
Aufgabe 2
Für einen Dieselmotor sollen mehrere Werte eines Zyklus berechnet werden. Nehmen Sie dafür den idealisierten Diesel-Kreisprozess:
- isentrope Kompression mit Volumenverhältnis 20
- isobare Verbrennung mit thermisch zugeführter Energie von 500 J
- isentrope Expansion
- isochorer, vollständiger Ersatz mit Frischluft
Der erste Schritt beginnt mit 0.5 Liter Luft bei einem Umgebungsdruck von 1 bar und einer Temperatur von 300 K.
- Skizzieren Sie ein qualitatives p-V- und T-S-Diagramm?
- Berechnen Sie Druck und Temperatur nach dem 1. Schritt.
- Um wie viel steigt die Temperatur im 2. Schritt?
- Berechnen Sie die mechanische Energie, welche die Luft im 3. Schritt abgibt.
Aufgabe 3
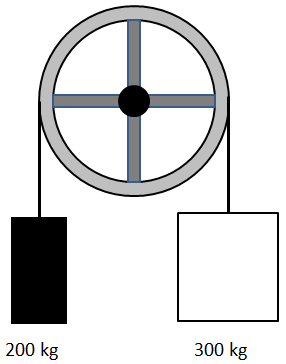
Ein Aufzug bestehe aus Kabine (Masse 300 kg), Antriebsrad (Durchmesser 2 m, Masse 200 kg, Massenträgheitsmoment 150 kgm2) und Gegengewicht (Masse 200 kg). Der Motor sei abgekoppelt und das Antriebsrad ist reibungsfrei drehbar. Wegen der Haftreibung des Seils auf dem Rad können die Seilkräfte an beiden Seilenden verschieden sein.
- Schneiden Sie die drei Körper frei, zeichnen Sie also die drei Körper einzeln, tragen Sie alle Kräfte ein, die auf die drei Körper einwirken (am besten mit drei verschiedenen Farben) und geben sie den Kräften passende Bezeichnungen.
- Führen Sie eine positive Bewegungsrichtung ein und formulieren Sie die für die Bewegung notwendigen Grundgesetze.
- Welche Beschleunigung erfährt die Kabine?
- Wie gross ist die Seilkraft auf das Gegengewicht?
Aufgabe 4
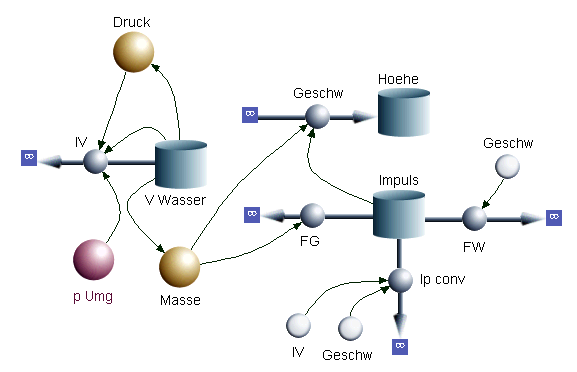
Das Systemdiagramm (Flowchart) zeigt das Modell eines Vertikalstarts einer Wasserrakete. Die Wasserrakete besteht hauptsächlich aus einer auf dem Kopf stehenden PET-Flasche (1.5 Liter, Durchmesser 85 mm), die mit Wasser (0.5 kg) und Druckluft gefüllt ist. Sobald die Öffnung (Durchmesser 21 mm) frei gegeben wird, drückt die Pressluft das Wasser nach unten weg und die Wasserrakete hebt ab.
- Wie wird die Volumenstromstärke berechnet? Wie wird sichergestellt, dass im Modell nicht mehr Wasser ausfliesst, als in der Flasche drin ist?
- Wie wird der konvektive Impulsstrom (Ip conv) berechnet?
- Wie könnte der Druck berechnet werden? Machen Sie einen Vorschlag und begründen sie diesen?
- Ergänzen Sie das Flowchart so, dass die vom Luftwiderstand dissipierte Energie berechnet wird. Schreiben Sie die entsprechenden Gleichungen dazu.
Aufgabe 5
Eine Weltraumstation besteht aus zwei konzentrischen Ringen. Der äussere Ring besitzt einen Aussendurchmesser von 150 m und ein Massenträgheitsmoment von 2.50 109 kgm2. Der innere Ring hat einen Aussendurchmesser von 100 m und ein Massenträgheitsmoment von 1.50 109 kgm2). Die beiden Ringe werden durch ein Antriebs-Brems-System in gegenläufige Rotation versetzt
- Wie schnell muss sich der äussere Ring drehen, damit sich am äusseren Rand ein Zentrifugalfeld der Stärke 5 N/kg einstellt? Geben Sie die Zeit für eine Umdrehung an.
- Wie viel Energie musste das Antriebssystem aufwenden, um die beiden Ringe aus dem Stillstand in den Rotationszustand von a) zu versetzen?
- Aus Sicherheitsgründen muss die Drehzahl der beiden Ringe innerhalb von vier Stunden halbiert werden. Wie gross ist das mittlere Drehmoment auf die beiden Ringe beim Abbremsen?
- Danach wird die Drehzahl mit konstanter Leistung in zwölf Stunden wieder auf den ursprünglichen Wert erhöht. Geben Sie die Grösse des Drehmoments auf die beiden Räder zu Beginn und am Schluss dieses Vorganges an.