Lösung zu Wärmepumpe mit zwei Wärmetauschern

Schema der WP mit zwei Wärmetauschern. Druckfehler am linken Rand, es muss heissen: Iw1 = 15 kW

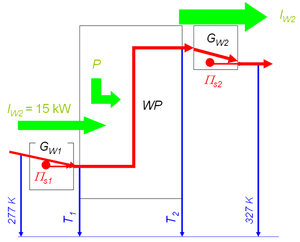
Dieses Modell einer Wärmepumpe besteht aus drei Teilen. In den beiden Wärmetauschern fliesst die Wärme von selbst von hoher zu tiefer Temperatur. Weil die Energie längs des Transportweges erhalten bleibt und die Entropie maximal zunimmt (total irreversibler Prozess), modelliert man die Wärmeleitung mit Hilfe der Energie. Der einfachste Ansatz (lineares Gesetz) ist hier hinreichend genau

[math] I_W = G_W \Delta T[/math]

Im mittleren Teil, der eigentlichen Wärmepumpe, wird die Entropie thermisch hinauf gepumpt. In einer idealen Wärmepumpe bleibt die Entropie erhalten. Die von der Wärmepumpe zu erbringende Prozessleistung ist gleich

[math] P = \Delta T I_S[/math]

Das Bild zeigt die drei Prozesse:

• erster Wärmetauscher: Energie bleibt erhalten, Entropie nimmt maximal zu
• ideale Pumpe: Entropie bleibt erhalten, Energie muss zugeführt werden
• zweiter Wärmetauscher: Energie bleibt erhalten, Entropie nimmt maximal zu

Der durch den ersten Wärmetauscher fliessende Energiestrom legt die untere Temperatur bei der Wärmepumpe fest

[math] I_{W1} = G_{W1} (T_0 - T_1)[/math] oder [math]T_1 = T_0 -\frac {I_{W1}}{G_{W1}}[/math] = 277 K - 15 kW / 1200 W/K = 264.5 K

Der bei der idealen Wärmepumpe ankommende Entropiestrom hat demnach eine Stärke von (zugeordneter Energiestrom durch Potenzial gleich Stärke des Trägerstromes)

[math] I_S = \frac {I_{W1}} {T_1}[/math] = 56.7 W/K

Am Ausgang der Wärmepumpe nimmt dieser Entropiestrom einen Energiestrom mit, der gleich Entropiestromstärke mal die dort herrschende, absolute Temperatur (T₂) ist. Kombiniert man diese Aussage mit dem Wärmeleitungsgesetz für den zweiten Wärmetauscher, erhält man die folgende Gleichung, die man dann nach T₂ auflöst

[math]I_{W2} = I_S T_2 = G_{W2} (T_2 - T_U)[/math], [math] T_2 = G_{W2} T_U / (G_{W2} - I_S)[/math] = 1000 W/K * 327 K /(1000 W/K - 56.7 W/K) = 347 K

Diese Gleichung liefert bei einer Umgebungstemperatur (T_U) von 327 K eine Ausgangstemperatur bei der idealen Wärmepumpe von 347 K. Multipliziert man diesen Wert mit der Stromstärke der gepumpten Entropie, erhält man einen zugeordneten Energiestom von I_W2 = 19.7 kW. Dieser Energiestrom geht ungehindert als Heizleistung an die 54°C warme Umgebung weg.

Die Entropieproduktionsrate des ganzen Systems ergibt sich aus der Differenz der beiden Entropiestromstärken

[math] \Pi_S = \frac{I_{W2}}{T_U} - \frac{I_{W1}}{T_0}[/math] = 60.2 W/K - 54.2 W/K = 6.0 W/K

Aufgabe