Himmelslift

Aus SystemPhysik
(Weitergeleitet von Space Elevator)
Die Druckversion wird nicht mehr unterstützt und kann Darstellungsfehler aufweisen. Bitte aktualisiere deine Browser-Lesezeichen und verwende stattdessen die Standard-Druckfunktion des Browsers.

Einsteigen, Knopf drücken - nächster Halt: Erdumlaufbahn. An einem 36 000 Kilometer langen Seil klettert die Kabine vom Äquator bis hinauf in den geostationären Orbit. Die Idee für einen Fahrstuhl ins All geht auf den russischen Raumfahrtpionier Konstantin Ziolkowski zurück. Inspiriert vom Pariser Eiffelturm entwarf er 1895 die grandiose Vision eines 36 000 Kilometer hohen Turms am Äquator. Den entscheidenden Gedanken hatte 1960 der russische Wissenschaftler Juri Artsutanow: Warum nicht das Gebäude weglassen? Das Tragseil des Fahrstuhls könnte man von einem geostationären Satelliten aus zur Erde herablassen und dann auf der Erde verankern. Zu breiter Popularität gelang die Idee 1978 durch den Roman "Fountains of Paradise" von Arthur C. Clarke, auf Deutsch unter dem Titel "Fahrstuhl zu den Sternen" erschienen.

Problemstellung

Konzeptskizze des Lifts

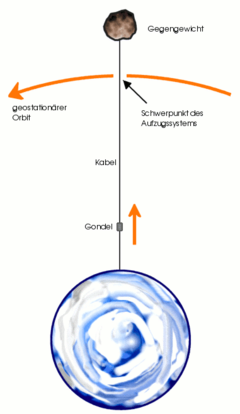
Wählt man die positive Richtung nach oben, bildet das Gravitationsfeld der Erde zusammen mit der Masse des Turms oder des Seils eine Impulssenke. Der Turm von Ziolkowski muss folglich den ans Gravitationsfeld weg fliessenden Impuls von der Erde her aufnehmen. Deshalb wird der Turm durch den nach oben, also vorwärts strömenden Impuls auf Druck belastet. An der Turmbasis ist die Impulsstromstärke oder Kraft am stärksten.

Das Gravitationsfeld der rotierenden Erde besteht aus zwei Teilen. Der eine Teil wird durch die Masse der Erde erzeugt und nimmt, falls die Erde als Kugel angesehen wird, mit dem Abstand vom Zentrum der Erde wie folgt ab

[math]g_G = -g_0 r_0^2 \cdot \frac {1}{r^2}[/math]

Der zweite Teil, die Stärke des Zentrifugalfeldes, hängt mit der Rotation der Erde zusammen und nimmt linear mit dem Abstand von der Erdachse zu

[math]g_z = \omega^2 \cdot r[/math]

Würde man auf einer Leiter sehr hoch steigen, könnte man spüren, wie das Gravitationsfeld immer schwächer wird. Bezüglich der erdfesten Leiter misst man ein Feld, das unten nach unten und oben nach oben zeigt

[math]g = \omega^2 \cdot r -g_0 r_0^2 \cdot \frac {1}{r^2}[/math]

An der Stelle, an der das Gravitationsfeld bezüglich der Erde verschwindet

[math]r_{gs} = \left(\frac {g_0 r_0^2}{\omega^2} \right)^{\frac {1}{3}}[/math] = 42'148 km

befinden sich die geostätionären Satelliten. Die geostationären Satelliten befinden sich demnach 35'770 km über der Erdoberfläche. Unterhalb der geostationären Bahn dominiert der Einfluss der Erdmasse, oberhalb die Rotation.

Das Seil von Artsutanow besitzt ein Gegengewicht, das sich ausserhalb der geostationären Bahn befindet. Dieses Gegengewicht wirkt als Impulsquelle, die bei geeigneter Dimensionierung den gesamten Impulsabfluss des Seilstücks unterhalb der geostationären Bahn kompensiert. Der von oben nach unten fliessende Impuls erreicht bei der geostationären Bahn die grösste Stromstärke. Dort ist das Seil am stärksten auf Zug belastet.

Doch schon Artsutanow erkannte, dass die Entwicklung eines geeigneten Tragseils das grösste Problem ist. Das Tragseil muss extrem reissfest und extrem leicht sein. Ein gewöhnliches Stahlseil würde bereits bei einer Länge von neun Kilometern unter der Last seines Eigengewichts zerreissen. Seit Anfang des 21. Jahrhunderts ist ein Material bekannt, das die Anforderungen erfüllen könnte: Kohlenstoffnanoröhren. Anfang 2004 ist es einem Wissenschaftlerteam um Alan Windle an der University of Cambridge gelungen, auf der Grundlage dieser Technologie einen etwa 100 Meter langen Faden herzustellen. Kohlenstoffnanoröhren haben ein bis zu 100 mal besseres Verhältnis von Zugfestigkeit zu Gewicht als Stahl, deshalb ist dieser Werkstoff ein möglicher Kandidat für den Weltraumlift. Jedoch ist die Technologie noch längst nicht ausgereift.

Impulsstrom

Impulsbilanz

Betrachtet man ein Stück Seil mit der Länge dr, dem Querschnitt A und der Dichte ρ, lautet die Impulsbilanz bezüglich dieses Stücks

[math]\Sigma_p + I_{p1} + I_{p2} = \rho A dr g - dI_p = 0[/math]

Σ steht für die Impulsquelle. Die Differenz der beiden Impulsstromstärken dIp entspricht der Quellenstärke und ist unterhalb der geostationären Bahn negativ, darüber positiv. Nach der Division mit dr erhält man die Gleichung

[math]\frac {dI_p}{dr} = \rho A g[/math]

Zylinder

Geht man von einem zylinderförmigen oder prismatischen Seil aus, kann die Gleichung auf die Impulsstromdichte, die (negative) Zugspannung σ, umgeschrieben werden

[math]\frac {dI_p}{\rho A} = -\frac {d\sigma}{\rho} = g dr[/math]

Im homogenen Gravitationsfeld (Gravitationsfeldstärke -g0) liefert die Integration über r

[math]\sigma = \rho g_0 \Delta r = \rho \Delta \varphi_G[/math]

Die maximale Zugspannung ist somit gleich Dichte mal Zuwachs des Gravitationspotenzials. Geht man bei einer Dichte von 7300 kg/m3 von einer zulässigen Zugspannung von 800 N/m2 aus, kann ein Seil höchstens 10 km lang sein.

Im inhomogenen Feld der rotierenden Erde gilt

[math]d\sigma = -\rho g dr = -\rho \omega^2 \cdot r dr + \rho g_0 r_0^2 \cdot \frac {1}{r^2} dr[/math]

Eine Integration diese Gleichung von der Erdoberfläche (rE = 6378 km) bis zur geostationären Bahn liefert

[math]\frac {\sigma}{\rho} = g_0 r_0^2 \left(\frac{1}{r_E} - \frac{1}{r_{gs}}\right) + \frac{\omega^2}{2}\left(r_E^2 - r_{gs}^2\right) = \Delta \varphi_G[/math] = 48.4 MJ/kg

Die Zugspannung pro Masse ist gleich der Änderung des Gravitationspotenzials. Für die Dichte von Stahl (7300 kg/m3) erhält man eine maximale Zugspannung von 350 kN/mm2

optimale Form

Man könnte auch ein Seil entwickeln, das überall die gleich Zugspannung σ aufweist. Ausgehend von der Impulsbilanz

[math]\frac {dI_p}{dr} = \frac {dA \sigma}{dr} = \rho A g[/math]

oder umgeformt

[math]\frac {dA}{A} = \frac {\rho}{\sigma} g dr[/math]

und aufintegriert, ergibt

[math]\ln \left( \frac {A_{gs}}{A_E} \right) = \frac {\rho}{\sigma} \cdot \left(g_0 r_0^2 \left(\frac{1}{r_E} - \frac{1}{r_{gs}}\right) + \frac{\omega^2}{2}\left(r_E^2 - r_{gs}^2\right)\right) = \frac {\rho}{\sigma} \cdot \Delta \varphi_G[/math]

Eine optimierte Form, bei welcher der Querschnitt exponentiell mit dem Gravitationspotenzial zunimmt

[math]A_{gs} = A_E e^{\frac {\rho}{\sigma} \Delta \varphi_G}[/math]

vermag die maximale Zugspannung nur mässig zu mindern. Um die vorgegebene Zugspannung am unteren Ende des Seils zu erzeugen, muss man das Seil im Boden verankert werden. Als Alternative käme auch ein zylindrisches Seilstück in Frage, das gemäss der weiter oben durchgeführten Berechnung die gewünschte Grenzspannung erzeugt.

Corioliskraft

Auf den auf- oder absteigenden Lift wirkt normal zum Seil in der Äquatorialebene eine Corioliskraft . Die Corioliskraft muss von einer Führungskraft, die vom Seil auf den Lift einwirkt, kompensiert werden

[math]F_F = F_C = 2mv\omega[/math]

Der während einer Fahrt zwischen Lift und Seil ausgetauschte Impuls ist unabhängig von der Geschwindigkeit des Liftes

[math]\Delta p = 2m\omega \Delta h[/math]

Die spezifische Impulsmenge (Impuls pro Kilogramm) beträgt für eine einzige Weltraumfahrt 5217 Ns/kg. Dieser Impuls muss im Tragseil nach unten oder oben, also seitwärts zur eigenen Bezugsrichtung, abgeführt werden. Infolge dieses Impulsabflusses weicht das Seil seitlich weg. Zudem muss der nach oben abliessende Impuls auf irgend einem Weg an die Erde zurückgeführt werden. Die Wirkung der Corioliskraft kann gemildert werden, indem man mindestens zwei Lifte betreibt, die sich gegenläufig bewegen.

Energiebetrachtung

Auf den Lift wirken vier Kräfte ein:

  • die Gewichtskraft (Summe aus Wirkung der Erdmasse und Erdrotation)
  • die Hubkraft (separates Zugseil oder auf dem Liftseil arbeitender Antrieb)
  • Corioliskraft (leistungsfrei)
  • Führungskraft (leistungsfrei)

Die Arbeit der Hubkraft ist gleich Liftmasse mal Änderung des Gravitationspotentials

[math]W(F_H) = -W(F_G) = m \Delta \varphi_G = m \left( g_0 r_0^2 \left(\frac{1}{r_E} - \frac{1}{r_{gs}}\right) + \frac{\omega^2}{2}\left(r_E^2 - r_{gs}^2\right)\right) = m[/math]*48.4 MJ/kg

Betrachtet man den Vorgang von einem erdfesten, aber nicht rotierenden Bezugssytem aus, ändert der Lift sowohl seine potentielle als auch seine kinetische Energie

[math]\Delta W = \Delta W_G + \Delta W_{kin} = m g_0 r_0^2 \left(\frac{1}{r_E} - \frac{1}{r_{gs}}\right) + \frac {m}{2} \omega^2 \left(r_{gs}^2 - r_E^2\right) = m[/math]*57.6 MJ/kg

Diese Energiebetrachtung, die in Schulbüchern leider oft gemacht wird, ist völlig sinnlos. Entweder befördert man einen Satelliten mit einer Trägerrakete nach oben oder man plaziert ihn mit dem Weltraumlift. Bei der Rakete sieht die Energiebilanz völlig anders aus und beim Lift ist die Hubarbeit etwa 16% kleiner als die berechnete Energiedifferenz. Der Grund für diese Differenz liegt bei der Führungskraft. In einem nichtrotierenden Bezugssytem muss die Arbeit der Führungskraft mit einbezogen werden. Eine Führungskraft ist nur bezüglich der Führungsvorrichtung (Schiene, Seil, Zahnstange) leistungsfrei. Hat die Führung selber eine Geschwindigkeit in Richtung der Kraft, ist die Leistung der Führungskraft, der zugeordnete Energiestrom ungleich Null. Die Arbeit der Hubkraft und die Arbeit der Führungskraft ergeben dann zusammen eine Energieänderung von 57.6 MJ pro Kilogramm Satellit. Aufwänden muss man aber nur die Arbeit der Hubkraft, also 48.4 kJ/kg.

Weblinks

Abgerufen von „http://systemdesign.ch/index.php?title=Himmelslift&oldid=8234“