Drehung
Ein starrer Körper kann um eine beliebige Achse gedreht werden. Dabei drehen sich alle Verbindungslinien auf dem Körper um den gleichen Drehwinkel. Wird der Körper mehrmals um die gleiche Achse gedreht, lassen sich alle Eigenschaften der Drehbewegung in einer Ebene, die normal zur Achse steht, untersuchen. Wird der Körper mehrmals um diese Achse gedreht, hängt die totale Drehung nicht von der Reihenfolge der einzelnen Operationen ab.
Die allgemeine Drehung eines Körpers wird durch die Richtung der Achse und den Drehwinkel beschrieben. Dreht man einen Körper mehrmals um verschiedene Achsen, hat die Reihenfolge der einzelnen Operationen einen wesentlichen Einfluss auf die Gesamtdrehung.
Mathematisch gesehen bilden die Drehopertionen eine Gruppe. Die Menge der Drehungen um eine festgehaltene Achse kann mit Hilfe der SO2, alle Drehungen im Raum mit Hilfe der SO3 beschrieben werden.
Drehung in der Ebene
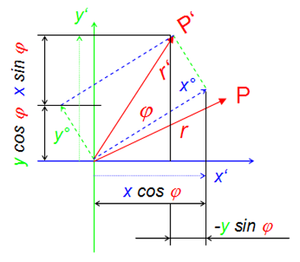
Bei einer ebenen Drehung gehe ein Punkt P in den Punkt P' und der zugehörige Orstvektor r in den Vektor r' über. Zerlegt man die mitgedrehten Komponenten des Ortsvektors x° und y° bezüglich des Koordinatensystems in je zwei eigene Komponenten, können die Komponenten des gedrehten Vektors (x' und y' ) aus den alten berechnet werden
[math]x' = x \cos \varphi - y \sin \varphi [/math]
[math]y' = x \sin \varphi + y \cos \varphi [/math]
Diese Drehung lässt sich mit Hilfe der Matrizenrechnung kompakt formulieren
[math]\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos \varphi \ -\sin \varphi \\ \sin \varphi \ \cos \varphi \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}[/math]