Hydromobil

Hydromobil

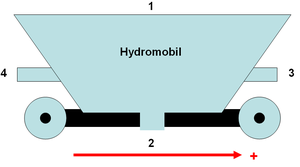
Das Hydromobil ist eine virtuelles Fahrzeug, an dem die Impulsbilanz bei offenen Systemen geübt werden kann. Das Hydromobil ist oben offen, damit es hinein fallendes Wasser aufnehmen kann (1). Unten besitzt es einen Auslass, durch den es Wasser ablassen kann (2). Vorne (3) und hinten (4) ist das Hydromobil mit je einem Rohr bestückt, durch das mittels einer Pumpe Wasser horizontal weg gespritzt oder angesaugt werden kann. Das Hydromobil kann in drei Modi betrieben werden. Im Modus frei rollt es reibungsfrei dahin. Im Modus fest sorgt ein geregelter Antrieb dafür, dass die Geschwindigkeit des Hydromobils auf einem konstanten Wert gehalten wird. Im Modus Reibung wirkt eine konstante Reibkraft an den Rädern gegen die Bewegung des Hydromobils.

Bilanzgleichungen

Die Impulsbilanz (Horizontalkomponente) bezüglich des Hydromobils lautet

[math]F+v_1I_{m1}+v_2I_{m2}+v_3I_{m3}+v_4I_{m4}=\dot p=\dot m v+m\dot v[/math]

Alle Geschwindigkeiten sind gegen das Bezugssystem zu messen. Ist die horizontale Geschwindigkeit des Wasserstromes gegen das Hydromobil (c_i) gegeben, gilt

[math]v_i=v+c_i[/math] i = 1, 2, 3, 4

Die Geschwindigkeit des vom Hydromobil aufgenommenen Wassers ist gleich Null, sobald dieses senkrecht herunter fällt. Die Geschwindigkeit des durch den Auslass (2) abfliessenden Wassers ist in der Regel gleich der Geschwindigkeit des Hydromobils, also gleich v.

Als zweite Gleichung benötigen wir noch die Massenbilanz

[math]I_{m1}+I_{m2}+I_{m3}+I_{m4}=\dot m[/math]

Im Modus fest fällt auf der rechten Seite der Impulsbilanz der Term mit der Beschleunigung weg, im Modus frei fehlt auf der linken Seite die Kraft und im Modus Reibung gilt

[math]F=-F_R\sgn(v)[/math]

Anwendungen

Rakete

Um die Bewegungsgleichung für eine reibungsfrei gleitende Rakete zu erhalten, ist nur der nach hinten gerichtete Massenstrom ungleich Null zu setzen. Auf die Indizierung der Ströme kann verzichtet werden

[math](v-c)I_m=\dot m v+m\dot v[/math]

Ersetzt man die Änderungsrate der Masse über die (triviale) Massenbilanz, folgt die Raketengleichung

[math]-cI_m=m\dot v[/math]

Man beachte, dass hier der Massenstrom bezüglich der Rakete negativ ist. Den Ausdruck -cI_m nennt man oft auch Schubkraft. Mit dieser Umschreibung kann die Rakete als Anwendung des Newtonschen Grundgesetzes verkauft werden, was natürlich grober Unfug ist.

Ersetzt man den Massenstrom zugunsten der Änderungsrate, ergibt sich eine etwas andere Formulierung der Raketengleichung

[math]-c\dot m=m\dot v[/math]

Seperation und Integration über die Zeit liefert die Geschwindigkeit der Rakete in Funktion der Masse

[math]v=v_0+c\ln\frac{m_0}{m}[/math]

Die Endgeschwindigkeit (Geschwindigkeitsänderung) der Rakete hängt in diesem Fall nur von der Ausströmgeschwindigkeit und der abgegebenen Masse ab. Ist die Restmasse kleiner als der e-te Teil der Anfangsmasse, übersteigt die Endgeschwindigkeit einer anfänglich ruhenden Rakete die Ausströmgeschwindigkeit. Vom Bezugssystem aus gesehen bewegt sich dann der austretende Massenstrom in Richtung der Rakete.

Güterwagen

Müssen ganze Eisenbahnzüge mit Schüttgut beladen werden, zieht die Lok die Wagen mit konstanter Geschwindigkeit unter dem Silo durch. Die Impulsbilanz nimmt dann die folgende Gestalt an

[math]F_{Res}=v\dot m[/math]

Die resultierende Kraft auf den zu beladenden Wagen ist gleich der Geschwindigkeit des Wagens mal die Änderungsrate der Masse, die wiederum gleich der Stärke des von oben zufliessenden Massenstroms ist. Weil dieser Massenstrom anfänglich nicht mit Impuls beladen ist, tritt er auf der linken Seite der Impulsbilanz nicht auf. Dem Wagen muss Impuls zugeführt werden (resultierende Kraft), damit die neu dazu kommende Masse entsprechend der Geschwindigkeit des Wagens mit Impuls beladen wird.

Würde eine Güterwagen mit Schüttgut beschickt, ohne dass eine horizontal gerichtete Kraft angreift (Mdous frei), gilt

[math]0=\dot m v+m\dot v[/math]

Die Beschleunigung ist dann gleich

[math]\dot v=-v\frac{\dot m}{m}[/math]

Die Geschwindigkeit des Güterwagens nimmt ab, weil der Impuls auf eine immer grösser werdende Masse verteilt werden muss.

Auto im Regen

Ein Auto fährt durch ein Gewitter. Wie viel zusätzliche Energie wird benötigt, um das Wasser auf die Geschwindigkeit des Wagens zu beschleunigen? Als Modell nehmen wir das Hydromobil im Modus fest. Die Massenströme 1 und 2 sind entgegen gesetzt gleich gross, die beiden andern gleich Null. Der eintretende Massenstrom bringt keinen Horizontalimpuls, der austretende nimmt Impuls mit (pro rata velocitatis). Damit nimmt die Impulsbilanz folgende Form an

[math]F+vI_{m2}=0[/math]

Der Massenstrom 2 hat einen negativen Wert, weil die Masse austritt. Nimmt man anstelle des austretenden den eintretenden Massenstrom und lässt den Index weg, ist die notwendige Antriebskraft gleich

[math]F=vI_m[/math]

Die Prozessleistung, um den zu F gehörenden Impulsstrom vom Boden ins Hydromobil zu pumpen, ist gleich

[math]P=vF=v^2I_m[/math]

Diese Prozessleistung ist doppelt so gross, wie der vom abfliessenden Wasser mitgenommene Energiestrom (nur der zur Horizontalbewegung gehörende Teil der kinetischen Energie)

[math]I_W=\frac 12 v^2I_m=\frac 12 \varrho v^2I_V=\varrho_{W}I_V[/math]

Die fehlende Hälfte wird beim Aufschlag des Wassers im Hydromobil oder beim Aufschlag des Regens auf das Auto dissipiert.

Bremshilfe

An der Erfindermesse in Genf (2008) ist eine pneumatische Bremshilfe für Autos vorgeschlagen worden. Sobald das Bremspedal stark gedrückt wird, strömt unter dem Auto Luft aus einer Druckflasche nach vorne weg. Dieser Vorgang entspricht einer "Schubumkehr" bei einer Rakete und kann mit dem Hydromobil (nur Massenstrom 3) nachgebildet werden. Die zugehörige Gleichung lautet dann

[math](v+c)I_m=\dot m v+m\dot v[/math]

Unter Verwendung der Massenbilanz vereinfacht sich die Gleichung zu

[math]c\dot m=m\dot v[/math]

Würde die Geschwindigkeit der ausströmenden Luft konstant bleiben, nimmt die Geschwindigkeit des Autos wie folgt ab

[math]v=v_0-c\ln\frac{m_0}{m}[/math]

Die Bremswirkung dieser "Erfindung" ist gering, weil nur ein kleiner Teil der Automasse in Form von Luft mitgeführt wird und die Luft - verglichen mit einem Raketentriebwerk - relativ langsam ausströmt. Aus diesem Grund wird die Wasserrakete vor dem Start zu einem Teil mit Luft (als Energiespeicher) und zu einem Teil mit Wasser (für den Impulstransport) gefüllt.

Strahltriebwerk

Strahltriebwerke pumpen Luft mit erhöhter Geschwindigkeit nach hinten weg. Die Zunahme der Masse im Gasstrom durch Zufuhr von Brennstoff kann in erster Näherung vernachlässigt werden. Um das Hydromobil zu einem Strahltriebwerk umzufunktionieren, setzen wir es unter Wasser. Im stationären Betrieb lautet die Impulsbilanz

[math]F_{Res}+v_3I_{m3}+v_4I_{m4}=0[/math]

Setzt man die Summe der beiden Massenströme gleich Null (Massenbilanz) und löst nach der resultierenden Kraft auf, folgt

[math]F_{Res}=(v_4-v_3)I_m\lt 0[/math]

Die mit der durchfliessenden Masse zu kompensierende Kraft hängt nur von der Stärke des Massenstromes und von Geschwindigkeitsdifferenz ab. Im Falle eines Strahltriebwerkes entspricht die resutierende Kraft bis auf den Luftwiderstand auf das Triebwerk der Schubkraft auf das Flugzeug

[math]F_S=(v_3-v_4)I_m[/math]

Bei ruhender Luft ist die Geschwindigkeit am Eintritt gleich Null und beim Austritt negativ. Man kann die Geschwindigkeiten auch vom Flugzeug aus analysieren. Die Geschwindigkeit 3 ist dann gleich minus die Geschwindigkeit des Flugzeuges und die Geschwidnigkeit 4 um den vom Triebwerk aufgebauten Wert kleiner

[math]F_S=(-v+v+\Delta v)I_m=\Delta vI_m[/math]

Ein Strahltriebwerk kann, um den gleichen Schub zu erzeugen, viel Masse über eine kleine Geschwindigkeitsdifferenz pumpen oder wenig Luft auf hohe Geschwindigkeit beschleunigen. Die dazu benötigte Leistung wird aber umso grösser, je stärker die Luft beschleunigt wird

[math]P=\frac 12\left((v+\Delta v)^2-v^2\right)I_m=\Delta v\left(v+\frac{\Delta v}{2}\right)I_m=F_S\left(v+\frac{\Delta v}{2}\right)[/math]

Die minimal mögliche Prozessleistung ist gleich der Leistung der Schubkraft. In diesem Grenzfall müsste das Triebwerk beliebig viel Masse ohne Geschwindigkeitsaufbau pumpen. Moderne Verkehrsflugzeug sind mit Turbofans ausgerüstet, deren Mantelstrom bis zu neun mal stärker als der Kernstrom ist. So kann viel Schub bei wenig Leistung erzeugt werden. Das Verhältnis von Leistung der Schubkraft zu Prozessleistung bezüglich des Massenstromes nennt man auch äusseren Wirkungsgrad

[math]\eta_{aussen}=\frac{P(F_S)}{P}=\frac{v}{\left(v+\frac{\Delta v}{2}\right)}=\frac{2v}{2v+\Delta v}[/math]

Knatterboot

Das Knatterboot ist ein Spielzeug mit Rückstossantrieb. Das Knatterboot stösst periodisch Wasser nach hinten weg, um danach wieder welches anzusaugen. Im Gegensatz zur landläufigen Meinung erzeugt sowohl der austretende wie auch der eintretende Wasserstrahl einen Rückstoss. Taucht man das Hydromobil unter Wasser und setzt es stellvertretend für das Knatterboot ein, lautet die Impulsbilanz unter Vernachlässigung der Relativbewegung des im Rohr enthaltenen Wassers bei konstant gehaltener Strömungsgeschwindigkeit c₄

[math]F_{Res}+v_4I_{m4}=F_{Res}+(v\mp c_4)I_{m4}=\dot m v+m\dot v[/math]

oder mit Hilfe der Massenbilanz umgeformt

[math]F_{Res}\mp c_4 I_{m4}=m\dot v[/math]

Ersetzt man die Stärke des Massenstromes durch das Produkt aus Dichte des Wasser, (negative) Ausströmgeschwindigkeit und Strahlquerschnitt A₄, folgt für die Beschleunigung

[math]\dot v=\frac 1m\left(F_{Res}+\varrho c_4^2 A_4\right)[/math]

Im Gegensatz zur Rakete ist diese Betrachtungsweie ein wenig gewagt, weil das sich im Rohr bewegende Wasser eine beachtliche Menge Impuls zu speichern vermag.

Lässt man für die Relativgeschwindigkeit c₄ beliebige Werte zu, nimmt die Impulsbilanz folgende Form an

[math]F_{Res}+(v-c_4)I_{m4}=F_{Res}+\varrho\left(c_4^2-vc_4\right)A_4=\dot p[/math]

Strömt Wasser von hinten ins Hydromobil ein (c₄ < 0), wird auf jeden Fall Impuls zugeführt. Solange das Hydromobil schneller fährt, als das Wasser nach hinten weg strömt, verliert dieses über das abgehende Wasser Impuls. Ist c₄ grösser als die Geschwindigkeit des Hydromobils wird wieder Impuls zugeführt.